[科普中国]-微分算子- · 科普中国网

在数学中，微分算子是定义为微分运算之函数的算子。首先在记号上，将微分考虑为一个抽象运算是有帮助的，它接受一个函数得到另一个函数（以计算机科学中高阶函数的方式）。1

描述在数学中，微分算子是定义为微分运算之函数的算子。首先在记号上，将微分考虑为一个抽象运算是有帮助的，它接受一个函数得到另一个函数（以计算机科学中高阶函数的方式）。

当然也有理由不单限制于线性算子；例如施瓦茨导数是一个熟知的非线性算子。不过这里只考虑线性情形。

记号最常用的微分算子是取导数自身。这个算子的常用记号包括：d/dx,D，这里关于哪个变量微分是清楚的，以及Dx，这里指明了变量。一阶导数如上所示，但当取更高阶n-次导数时，下列替代性记号是有用的：dn/dxn,Dn,Dxn。1

记号D的发明与使用归于奥利弗·亥维赛，他在研究微分方程中考虑了如下形式的微分算子

另一个最常见的微分算子是拉普拉斯算子，定义为

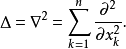另一个微分算子是Θ算子，定义为

有时候这也称为齐次算子，因为它的本征函数是关于z的单项式：

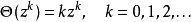在n个变量中齐次算子由

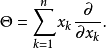给出。与单变量一样，Θ的本征空间是齐次多项式空间。

性质（1）微分是线性的，即1

D(f+g)=(Df)+(Dg)

D(af)=a(Df)

这里f和g是函数，而a是一个常数。

（2）任何以函数为系数之D的多项式也是一个微分算子。我们也可以通过法则

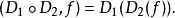
（3）复合微分算子。需要一些注意：首先算子D2中的任何函数系数必须具有D1所要求的可微次数。为了得到这样运算的一个环，我们必须假设所用的系数的所有阶导数。第二，这个环不是交换的：一个算子gD一般与Dg不同。事实上我们有例，如在量子力学中的基本关系：

Dx-xD=1

但这些算子的子环：D的常系数多项式是交换的。它可以另一种方式刻画：它由平移不变算子组成。

（4）微分算子也服从移位定理（shift theorem），即

算子的伴随给定一个线性微分算子T，，这个算子的伴随定义为算子使得

这里记号表示数量积或点积。从而此定义取决于数乘的定义。

单变量在平方可积函数空间中，数量积定义为

如果另外增添要求f或g当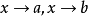等于零，我们也可定义T的伴随为

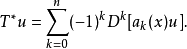
此公式不明显地取决于数量积的定义，故有时作为伴随算子的一个定义。当用这个公式定义时，它称为T的形式伴随。

一个（形式）自伴算子是与它的（形式）伴随相等的算子。

多变量如果Ω是R中一个区域，而P是Ω上一个微分算子，则P在L(Ω)中的伴随由对偶性以类似的方式定义：

对所有光滑L函数f与g。因为光滑函数在L中是稠密的，这在L的一个稠密子集上定义了伴随：: P是一个稠定算子。

例子施图姆-刘维尔算子是形式自伴算子一个熟知的例子。这个二阶微分算子L可以写成如下形式

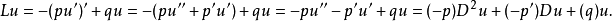这个性质可用上面的形式自伴的定义来证明。

应用在物理科学的应用中，像拉普拉斯算子在建立与求解偏微分方程中起着主要的作用。

在微分拓扑中，外导数与李导数算子有内蕴意义。

在抽象代数中，导子的概念是微分算子不要求分析的一个推广。通常这样的推广用于代数几何与交换代数。