[科普中国]-全等关系

在平面几何里，如果两个图形不仅形状相同，而且大小也相等，能够完全重合，则这两个图形为全等形。两个全等形之间的关系称为全等关系。

基本内容一个图形经过平移、翻折、旋转后，位置变化了，但形状和大小都没有改变，即平移、翻折、旋转前后的图形全等。即一个图形经过平移、旋转或翻折等变换后，所得到的新图形一定与原图形全等。反过来，两个全等的图形经过平移、旋转或翻折变换后一定可以重合。两个全等形之间的关系称为全等关系。1

比较相似形：形状相同的两个图形称作相似形。

全等形：若两个图形不仅形状相同，而且大小也相等，能够完全重合，那么二者全等。

两者的关系：两个相似形未必是全等形；两个全等形一定是相似性。全等形是特殊的相似形。例如，全等三角形是相似三角形当相似比等于1时的特例，因而全等形与相似形之间体现了从特殊到一般关系的推广。

相似关系：两个相似形之间的关系为相似关系。

全等关系：两个全等形之间的关系为全等关系。1

特点全等形的特点是形状、大小相同。如果已知两个图形之间存在全等关系，即可知这两个图形的形状、大小均相同。2

例1：图1中的图形的形状、大小相同，为全等形，它们之间为全等关系。

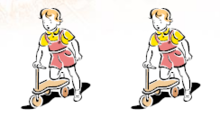
例2：图2中的图形的形状相同，大小不同，为相似形，它们之间为为相似关系，而不是全等关系。

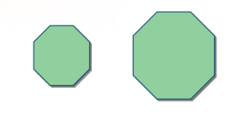
相关计算例1.已知图3中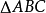， 与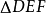 之间为全等关系，AB=4，求DE长度。

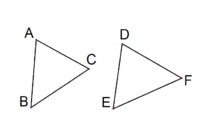
解：由全等关系可知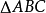， 与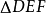 为全等三角形，由全等形的性质可知AB=DE=4。

教学应用在全等关系的数学教学中可以采用“探究法”。“探究法”的精髓在于以学生为主角，使他们由被动地接受知识转变为知识的探索者。通过亲自动手，积极思考，热烈讨论，探索知识，学生能更加深入理解知识的内涵，并培养观察力、思维能力、动手能力、归纳能力、语言表达能力和创造能力等。“探究式教学法 ”是指在老师的指导下 ，学生通过具体的操作，亲自尝试后，经过积极思考和讨论，找到知识的规律，总结出结论，学会新知，并发展思维、培养能力的综合教学方法。通过让学生对全等和相似进行区分，可以引导学生对全等形与相似形之间的关系进行积极思考，从而得到两个相似形之间的关系为相似关系，两个全等形之间的关系为全等关系的结论，从中拓展学生思维、提高学生独立思考的能力。3

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学