[科普中国]-震级

**震级：**是指地震大小，通常用字母M表示。地震愈大，震级数字也愈大，世界上最大的震级为9.5级。它是根据地震波记录测定的一个没有量纲的数值，用来在一定范围内表示各个地震的相对大小（强度）。震级与地震烈度的概念根本不同。震级代表地震本身的强弱，只同震源发出的地震波能量有关；烈度则表示同一次地震在地震波及的各个地点所造成的影响的程度，与震源深度、震中距、方位角、地质构造以及土壤性质等许多因素有关。用地震释放的能量来表示地震的大小，即地震的震级。震级大的地震，释放的能量多；震级小的地震，释放的能量少。中国一般采用里氏震级。通常小于2.5级的地震称为小地震，2.5-4.7之间的地震称为有感地震。震级每相差1.0级，能量相差大约30倍。

发展历史里氏地震规模最早是在1935年由两位来自美国加州理工学院的地震学家里克特（Charles Francis Richter）和古登堡（Beno Gutenberg）共同制定的。

此标度原先仅是为了研究美国加州地区发生的地震而设计的，并用伍德·安德森扭力式地震仪（Wood-Anderson torsion seismometer）测量。里克特设计此标度的目的是区分当时加州地区发生的大量小规模地震和少量大规模地震，而灵感则来自天文学中表示天体亮度的星等。

为了使结果不为负数，里克特定义在距离震中100千米处之观测点地震仪记录到的最大水平位移为1微米（这也是伍德-安德森扭力式地震仪的最大精度）的地震作为0级地震。按照这个定义，如果距震中100千米处的伍德-安德森扭力式地震仪测得的地震波振幅为1毫米（103微米）的话，则震级为里氏3级。里氏地震规模并没有规定上限或下限。现代精密的地震仪经常记录到规模为负数的地震。

由于当初设计里氏地震规模时所使用的伍德·安德森扭力式地震仪的限制，近震规模 ML 若大于约6.8或观测点距离震中超过约600千米便不适用。后来研究人员提议了一些改进，其中面波震级（MS）和体波震级（Mb）最为常用。

最初的原始震级标度只适用于近震和地方震。1945年B.古登堡把震级的应用推广到远震和深源地震，奠定了震级体系的基础，利用宽频带地震仪记录远震传来的面波，根据面波的振幅和周期来计算震级。

震级强弱

地球上的地震有强有弱。用来衡量地震强度大小的尺子有两把，一把叫地震震级；另一把叫地震烈度。举个例子来说，地震震级好象不同瓦数的日光灯，瓦数越高能量越大，震级越高。烈度好象屋子里受光亮的程度，对同一盏日光灯来说，距离日光灯的远近不同，各处受光的照射也不同，所以各地的烈度也不一样。

地震震级是衡量地震大小的一种度量。每一次地震只有一个震级。它是根据地震时 释放能量的多少来划分的，震级可以通过地震仪器的记录计算出来，震级越高，释放的能量也越多。中国使用的的震级标准是国际通用震级标准，叫“里氏震级”。

分类地震按震级大小的分类情况：弱震：震级小于3 级的地震；

有感地震：震级等于或大于3级、小于或等于⒋5级的地震；

中强震：震级大于⒋5级，小于6级的地震；（如彝良地震）

强震：震级等于或大于6 级的地震（如玉树地震）。其中震级大于或等于8 级的又称为巨大地震（如汶川地震）。

国际上使用的地震震级——里克特级数，是由美国地震学家里克特所制定，它的范围在 1 — 10 级之间。它直接同震源中心释放的能量（热能和动能）大小有关，震源放出的能量越大，震级就越大。

测定方法中国的面波震级计算公式为：

地震震级 M ，用地震面波质点运动最大值 (A/T)max 测定。计算公式为：

M=lg(A/T)max+ σ ( Δ )

式中： A 地震面波最大地动位移，取两水平分向地动位移的矢量和，μ m ；

T 相应周期， S ；

Δ震中距， ( 度 ) 。

测量最大地动位移的两水平分量时，要取同一时刻或周期相差在1/8周之内的震动。若两分量周期不一致时，则取加权和：

T=(T N ×A N +T E× A E )/(A N +A E )

式中： A N 南北分量地动位移，μ m；

A E 东西分量地动位移，μ m；

T N A N 的相应周期， S ；

T E A E 的相应周期， S ；

量规函数σ ( Δ ) 为：

σ ( Δ )=1.66lg Δ +3.5

不能使用与表一中给出的值相差很大的周期来测定地震震级 M 。地震震级 M 应根据多台的平均值确定。

式中A为两水平分向地动位移的矢量合成振幅，以微米为单位；T为相应的周期，以秒为单位；σ（Δ°）为面波震级起算函数，只与震中距Δ°(测点与震中间的大圆弧度数)有关；Cs为台站校正值。

面波震级标度Ms比较适用于从远处（震中距大于1000千米）测定浅源大地震的震级，而且各国地震机构的面波震级测定结果也比较一致，因此世界各国在公布1931年新疆8级地震和交换有关震级的信息资料时 ，一般都使用面波震级。即通常所说的里氏震级。另外，为解决巨大地震的面波震级饱和问题，有人提出用震源物理中的地震矩概念推导出一种新的震级标度——矩震级MW。智利大地震的面波震级 Ms=8.5，但矩震级MW=9.5，成为人类已知的最大地震。矩震级已在地震观测中开始试用，但其方法还在进一步研究和完善。它可作为面波震级的有益补充，但不能完全取代面波震级。

震级标度地震发生后，人们首先关心的问题是：这是多大的地震？如果回到几百年前，我们肯定得不到像“×级地震”的类似答案，而是一系列关于地震破坏的宏观描述，犹如明史中记载的陕西华县地震：“……地裂泉涌，中有鱼物，或城郭房陷入地中……官吏、军民压死八十三万有奇”。也就是说，那个时候，我们只能根据地震的破坏程度——烈度来估计地震的大小。烈度不仅受人的主观影响，还与震区的地质、建筑条件等因素有关，因此，烈度并不能定量地度量地震大小。

1935年，查尔斯·里克特在研究美国南加州地震时，发明了一种定量测量地震大小的方法。他规定在震中距为100km的地方，如果“标准地震仪”（伍德—安德森地震仪，周期是0.8s，放大倍数为2080）记录到的地震波最大振幅是1微米（注：仪器上记录到1微米对应的实际地动位移是1/2080=0.00048微米），震级为0；如果振幅是x微米，震级为其对数。当然，当振幅是0.1微米时，震级为lg0.1=-1，相当于小锤子敲打地面产生的震级。实际上，绝大多数地震仪不会恰好都摆在100km震中距的地方，此时就要根据震中距对应的量规函数来校正数值。里克特提出的这种震级标度被后人称为里氏震级ML，也叫地方性震级，主要适用于6级以下的中小地震，这里的L表示local（地方性）的意思。

里氏震级的出现，第一次把地震大小变成了可测量、可相互比较的量，为地震学的定量化发展奠定了基础。迄今为止，伍德—安德森地震仪早已绝迹，成为博物馆的陈列品。但人们为了保持地震记录的对比和延续性，很多小地震仍会通过仪器的模拟仿真，计算出里氏震级。

伍德—安德森地震仪是一种短周期地震仪（周期为0.8s），它可以较好地记录短周期地震波。但地震波在传播过程中，由于高频地震波（即短周期波）的衰减速度要远远大于低频地震波，当地震仪距离震中较远时，这种地震仪的记录能力变得有限。1945年，地震学家古登堡发明了面波震级Ms，Ms可以远距离记录地震，这就弥补了里氏震级的不足。其中，s表示surface wave（面波），它是根据周期约为20s的面波大小确定的地震震级。

面波震级也存在问题，当地震的震源深度较深的时候，激发的面波不显著。所以，古登堡还发明了体波震级mb，b表示body wave（体波），它是根据地震波的体波（通常是P波）的大小确定的地震震级。几乎所有的地震，无论距离远近、震源深度，还包括核爆炸，都可以在地震图上较清楚地识别P波，因此mb具有广泛的应用，美国地质调查局（USGS）对外公布的很多震级就是mb。

遗憾的是，无论是里氏震级、面波震级、还是体波震级，都存在着两个主要问题。一是这些震级与地震发生的物理过程没有直接联系，物理含义不清楚。二是通过统计分析，发现它们具有“饱和”现象。也就是说，当地震所释放的能量增大的时候，震级却不再增大（见图），因此面对大地震时，采用这些震级标度会低估地震的能量。

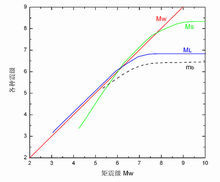【矩震级（Mw）与里氏震级（ML）、面波震级（Ms）及体波震级（mb）的关系】

1979年，日本的金森博雄提出了矩震级Mw的概念。矩震级的计算公式中用到了地震矩M0，地震矩具有严格的物理意义，其中M0=uAD（u是剪切模量，A是破裂面的面积，D是地震破裂的平均位错量）。从公式看，地震破裂面面积越大，位错量越大，释放的能量也就越多。正因为如此，矩震级不会像其他震级一样存在饱和问题。比如1960年智利大地震，测定的矩震级Mw=9.5，而面波震级已经饱和，仅为8.5。

矩震级已成为世界上大多数地震台网和地震观测机构优先推荐使用的震级标度。不过，由于世界各国有各自的震级研究历史和计算公式，各国对外公布的震级标度还未统一。中国对外公布的震级大多是面波震级而不是矩震级。比如这次日本大地震，中国公布的是面波震级8.6级，美国公布的是矩震级9.0级。

震级能量假定第1级地震所释放的能量为1，第2级应为31.62，第3级应为1000，依此类推，第7级为10亿，第8级为316.2亿，第9级则为10000亿。由于里氏地震规模是常用对数，因此在估算能量的时候，里氏震级每增加一，释放的能量大约增加32倍。

下表列出的是不同级别的地震释放的能量相当于的TNT当量：

|| ||

发生频率下表列出的是不同里氏震级（ML）的年均发生次数和震中地区的影响：

|| ||

拓展《利用高频GPS确定大地震震中和震级研究：2008年汶川8.0级地震应用结果》1

本词条内容贡献者为:

郝庆菊 - 副教授 - 西南大学