[科普中国]-弹性势能

性能介绍

物体由于发生弹性形变，各部分之间存在着弹性力的相互作用而具有的势能叫做“弹性势能”。在工程中又称“弹性变形能”。例如，被压缩的气体、拉弯了的弓、卷紧了的发条、拉长或压缩了的弹簧都具有弹性势能。

弹性势能是存储在材料或物理系统的构造中的潜在机械能，因为执行工作以扭曲其体积或形状。当需要压缩和拉伸或大体上以任何方式变形时，弹性能量就会发生。 弹性理论主要发展为固体和材料力学的形式1（注意，拉伸橡皮筋所做的工作不是弹性势能的一个例子，它是熵弹性的一个例子）弹性势能方程用于机械平衡位置的计算。 在数学上，方程可以表示为2：

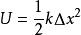
势能的单位与功的单位是一致的。确定弹力势能的大小需选取零势能的状态，一般选取弹簧未发生任何形变，而处于自由状态的情况下其弹力势能为零。弹力对物体做功等于弹力势能增量的负值。即弹力所做的功只与弹簧在起始状态和终了状态的伸长量有关，而与弹簧形变过程无关。弹性势能是以弹力的存在为前提，所以弹性势能是发生弹性形变，各部分之间有弹性力作用的物体所具有的。如果两物体相互作用都发生形变，那么每一物体都有弹性势能，总弹性势能为二者之和。

弹性的本质是可逆性。应用于弹性材料的力将能量转移到材料中，在将能量转移到其周围环境之后，能够恢复其原始形状。然而，所有材料对于它们可以承受的变形程度都有限制，而不会破坏或不可逆地改变其内部结构。因此，固体材料的特征包括通常在应变方面的弹性极限的规格。超过弹性极限，材料不再以弹性能量的形式储存在其上进行的机械作业的所有能量。

物质内或物质内的弹性能量是构型的静态能量。它对应于主要通过改变核之间的原子间距离而存储的能量。热能是材料内动能的随机分布，导致材料关于平衡构型的统计波动。但是有一些互动。例如，对于某些固体物体，扭曲，弯曲和其他变形可能会产生热能，导致材料的温度升高。固体中的热能通常由称为声子的内部弹性波进行。孤立物体规模较大的弹性波通常产生足够缺乏随机化的宏观振动，它们的振荡仅仅是物体内的（弹性）势能与整体物体的运动动能之间的重复交换。

实际应用机械系统中的弹性势能

如果机械系统的组件施加到系统上时发生变形，那它们将存储弹性势能。任何时候，在其外部的力移动或变形物体时，能量转移到物体（即在其上进行作业）。通过作业传递到物体的能量的量被计算为力的矢量点积和物体的位移。当力被施加到系统时，它们在内部分配到其组成部件。虽然一些能量转移可以最终存储为获得的速度的动能，但是成分物体形状的变形导致存储的弹性能量。

原型弹性部件是螺旋弹簧。弹簧的线性弹性表现由比例常数参数化，称为弹簧常数。该常数通常表示为k（参见胡克定律），并且取决于线圈形成的材料的几何形状，横截面积，未变形的长度和性质。在一定的变形范围内，k保持恒定，并被定义为位移与由该位移产生的弹簧恢复力的大小的负比率。3

公式计算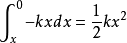 其中，k为弹性系数，x为形变量。注意：此公式中的x 必须在弹簧的弹性限度内。

弹力做功与弹性势能变化的关系：弹性势能是弹力做功转化而来，弹力做正功，弹性势能减少，弹力做负功，弹性势能增加。弹性势能的定义：发生弹性形变的物体各部分之间，由于有弹力的相互作用而具有势能，这种势能就是叫做弹性势能。

我们还可以从另外一种角度看弹力做功问题，功=力X距离。我们知道力和距离的图象中，曲线围成的面积就是做的功的大小。弹性力和距离的轴围成的图形是三角形，那么就是三角形的面积公式： 。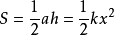

但是我们不能错误的认为弹力做功就是弹性势能，功是功，能是能，做功伴随能量的变化，功不是能。

能的关系弹性势能可与动能直接相互转化，但不能与重力势能直接转化。核心或实质：（势能和动能间之间可直接转化，但势能不能与势能直接相互转化，就是说不可能在动能不变的情况下转化）