[科普中国]-诱导速度

概论

诱导速度是指空气在流过某一物体后产生额外的速度，比如空气在经过物体前速度为V0，经过该物体后速度变为V1，那么vi=V1-V0即为诱导速度。

对于我们直升机而言，旋翼与空气相互作用，空气因受旋翼作用而加速向下流动，空气速度增加量就是该处的诱导速度值，同时空气给旋翼与反作用力，即旋翼产生的拉力。直升机悬停时，由于空气（桨盘上方无穷远处）原来没有速度，那么在桨盘下方的气流速度就是诱导速度。

诱导速度与旋翼拉力，需用功率，飞行状态关系密切。一般简化计算均假设诱导速度均匀分布，而实际上诱导速度在空间不同位置是变化的。因此精确计算必须对诱导速度大小，分布规律的研究计算。

直升机垂直飞行时的诱导速度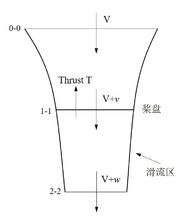直升机在作垂直上升飞行时，0-0截面位于滑流区上游无穷远处，该截面处气流速度为直升机垂直上升速度 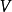。而在1-1截面处，气流经过桨盘后获得了一个增量 ，速度变为 ，并且。气流流动至下游很远处的2-2截面后，速度则变为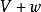 。这里， 为桨盘处的诱导速度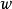， 为下游很远处的诱导速度。1

对旋翼滑流应用定常条件下的动量定理，不计空气重量，设桨盘对气流的作用力为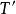 。假设气流是无粘的，因此，滑流边界上无切向力，仅受法向压力。滑流是轴对称的，其整个侧面上压强的水平横向分量自相平衡，而轴向分量构成的总压力与滑流上游0-0和下游2-2截面所受的总压力互相平衡。因而，滑流所受外力合力为 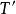，而轴向速度由 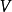增加至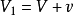 ，再继续变为 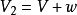，根据动量定理，可得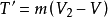： ，式中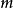 为单位时间内流过滑流任一截面的空气质量。那么，旋翼的拉力为 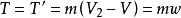，拉力的方向与滑流增速方向相反。

其次，对旋翼滑流应用定常条件下的能量守恒定律，仍不计重力。因为滑流上游处截面0-0与下游处截面2-2压力所做的功率互相抵消，而侧壁压强与流速垂直，功率为0。所以，滑流的动能变化所需能量完全来自旋翼。那么，旋翼所消耗功率就可由滑流的动能变化率确定：

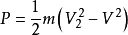
旋翼付出的功率则应为：

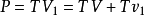
从式中可以看出，旋翼功率等于旋翼拉力与桨盘处气流速度的乘积。在滑流理论中，该功率还可分为两部分：一部分是拉力与运动速度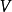 的乘积，称为“有效功率”；另一部分是拉力与桨盘处诱导速度 的乘积，称为“诱导功率”，纯为损失。

联立以上三式，可得

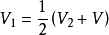或

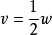
桨盘处的气流速度，等于桨盘上游与下游处气流速度之和的一半。也可表示为桨盘处的诱导速度，等于桨盘下游处诱导速度的一半。1

而对于直升机垂直下降的状态，其气流速度方向发生了变化，并且在桨盘上游很远处出现诱导速度，而桨盘下游很远处的气流速度则为垂直下降的速度。2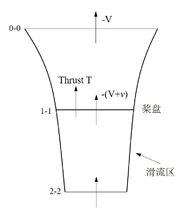

直升机前飞时的诱导速度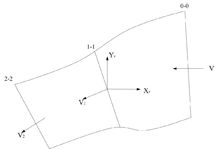

直升机前飞时，处于斜流状态，未扰动气流经过桨盘后，不仅气流速度大小改变，而且气流速度方向也有偏转，因此，任一截面处的气流速度都是未扰动气流速度与诱导速度的矢量和。将气流速度与气动力分解至速度坐标系。

上游0-0截面处气流速度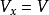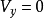： ， ；诱导速度： ， 。

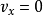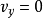桨盘1-1截面处气流速度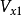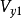： ， ；诱导速度： ， 。

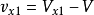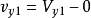下游2-2截面处气流速度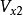 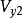， ；诱导速度： ， 。

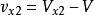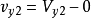由动量定理有

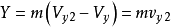
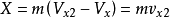式中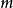 为空气质量流量，各截面处的 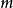均相等。

再根据动能定理，可得沿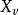 和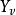 方向的功率为

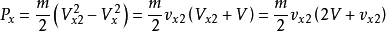
联立以上各式可得

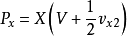
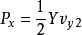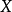式中和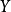分别为旋翼向前的推力和旋翼升力。

于是，可得

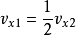
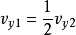
那么桨盘处诱导速度

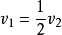
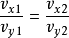
由此可得出结论：在斜流状态，旋翼桨盘处的诱导速度在数值上等于下游很远处的诱导速度的一半，在方向上两者彼此平行。1