[科普中国]-滚动接触理论

简介

由于滚动接触问题的系统研究始于轮轨接触问题的研究，当前常用的滚动接触问题解决方法多来自轮轨接触研究领域，因此，下面主要介绍轮轨滚动接触理论。轮轨滚动接触理论（theory of wheel-rail rolling contact）研究轮轨滚动接触行为的理论。轮轨滚动接触理论是研究列车运行时，轮轨相对运动状态和接触斑上作用力的关系。接触斑上的作用力包括其大小、方向和分布。

接触理论的创始人是Hertz Heinrich，1882年他在德国一家杂志上发表了具有开创性的论文“论弹性固体的接触”。他对接触问题的研究起因于对玻璃间光学干涉的试验，两个轴线成45°的圆柱形玻璃透镜受压后发生弹性变形，从弹性变形对干涉条纹图像存在的影响提出了接触压力呈椭圆形分布的假设。这一结论一直在铁路轮轨、齿轮、轴承等工业的发展中起着重要的作用。实际上Hertz理论作了如下简化：接触物体被看作弹性无限半空间，接触载荷仅仅作用在平面上一个小的椭圆区域上，接触体内在接触区附近应力分布是高度集中的，并和物体接触区附近的几何尺寸有关。这就要求接触区几何尺寸远小于物体的几何特征尺寸和接触区附近的曲率半径。Hertz在研究中，又假设接触表面是光滑的，无摩擦效应，接触物体表面仅传递法向力。Hertz接触理论为后来的接触理论及滚动接触理论的发展奠定了理论基础。

这属于静态接触问题，但是铁路车轮在轨道上运动属于滚动接触问题，其研究比静态接触研究复杂。

最“经典”的解决滚动接触问题的方法可追溯到Carter和Fromm H.。1926年，Carter发表了著名论文“论机车动轮行为”，他将铁路钢轨看成弹性半空间，用弹性圆柱体模拟车轮，并将两者材料常数取为一致，借助于Hertz理论和弹性半空间理论求解这二位弹性体滚动接触问题，很巧妙地给出接触斑中黏着区和滑动区的划分、作用力的大小和分布以及轮轨之间纵向切向力和蠕滑率的关系定律。他最大的贡献是他的研究思路和方法为三维弹性体滚动接触理论研究提供了有效手段。

接触力学是研究两个表面接触的固体相互作用所产生的应力和应变的力学。当两个接触体的接触点产生相对运动并传递力和力矩时，就出现有别于静态接触的滑动和滚动接触。铁道车轮在轨道上运转时，接触表面上的质点以滑动和滚动相结合的方式作相对运动。对轮轨滚动接触及其传递牵引力的研究，使滚动接触理论得以不断深入和发展。围绕轮轨滚动接触问题的求解，研究发展了许多理论模型，统称轮轨滚动接触理论。较著名的理论有Carter 理论，Vermeulen-Johnson理论，kalker线性理论，kalker简化理论，kalker三维精确理论，沈氏理论等。

Hertz接触理论最早对两个弹性体接触处应力状态的令人满意的分析，是由Hertz在1882年首先做出的，当时他正在研究两个圆柱透镜之间间隙中的Newton光学干涉条纹，他注意到由于透镜之间的接触压力对透镜表面弹性变形可能造成的影响。Hertz发现两个半径为R，轴线交角为45°的圆柱透镜在未加载的情况下，它们之间的干涉条纹显示出椭圆形等值线特征，如图 1所示。从加载条件下的光学干涉条纹图2不难想象接触面保持椭圆型区域，于是提出了接触压力呈椭圆形分布的假设。

Hertz用弹性力学理论研究两个弹性体的接触问题，提出了弹性接触的Hertz理论。Hertz理论中引入了以下假设：(1)表面外形函数以及它的一阶和二阶导数在接触区都是连续的，并且是非协调的；(2)小应变；(3)接触区域的有效尺寸比起每个物体的尺寸和接触表面的相对曲率半径是很小的，因此每个接触物体可被看作是一个半空间；(4)表面无摩擦的，两个表面之间只传递法向压力。

Hertz接触理论是建立在无摩擦的弹性接触面上，所以，它只能对轮轨接触的法向力进行计算。但由于其形式简单和使用方便，许多研究人员仍使用它进行轮轨接触问题的计算。

Carter和Fromm的二维弹性接触理论该理论基于Hertz接触条件，即接触表面是光滑的、车轮和轨道看成是弹性半空间，接触斑是平表面的；轮轨接触点及附近的曲率半径看作常数，接触斑的形状是椭圆，正压力是半椭球状。

英国学者F. W. Carter于1926年发表论文《论机车动轮的行为》，研究带有摩擦的二维滚动接触理论。轮轨间接触椭圆的形状在很大程度上取决于车轮的磨耗程度和轨头的形状，并符合按Hertz理论所求的接触斑椭圆的变化规律。新轮、新轨相接触时，其接触椭圆沿纵向的半轴通常大于沿横向的半轴。然而，当轮轨在运用中磨耗后，其接触椭圆与上述比对，相当于转过90°，即纵向半轴小于横向半轴，可将它近似成二维的长方形条带。因此，Carter在研究时就假定车轮为一圆柱体，而钢轨为一半径无限大的圆柱，则将轮和钢轨的关系看成圆柱在无限半空间弹性体表面上的滚动，并将两者的弹性常数取为一致。建立边界条件后，Carter用半空间逼近圆柱体，并求解两个半空间接触的二维弹性（平面应变）问题。Fromm考虑的是两个具有相同弹性常数的圆柱体的滚动接触问题，并且在不用半空间近似的情况下，成功地求解这个二维弹性问题。

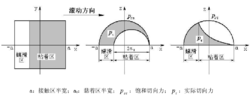Carter和Fromm都假设接触力中的切向摩擦力满足Coulomb摩擦定律，并且均将法向应力分布取为Hertz分布，它们还假设整个接触区域上有滑动，且方向相同。两位作者都假设：接触区分为两部分，即邻接前沿的区域，滑动为零的黏着区；和其他邻接后沿的区域，有滑动的滑动区。Carter对接触区域的划分如图 3所示。

Carter的滚动接触理论模型虽然只能解决二维接触问题，但非常实用，至今仍为铁路工程技术人员使用，他的研究最大贡献是他的研究方法和思路为后来的学者（Johnson、Kalker等）进行三维弹性体滚动接触理论研究提供有效手段。其缺点是它不能处理自旋蠕滑，也不能得到三维情形下的无自旋解。

Kalker简化理论该理论基于Hertz接触条件，即接触表面是光滑的、车轮和轨道看成是弹性半空间，接触斑是平表面的；轮轨接触点及附近的曲率半径看作常数，接触斑的形状是椭圆，正压力是半椭球状。

在轮轨蠕滑理论研究方面作出很大贡献的是荷兰学者Kalker教授。他于1967年在他的博士论文中，用级数方法讨论了具有椭圆形接触区的三维滚动接触问题，研究中考虑了纵横向蠕滑率和自旋蠕滑率对接触斑蠕滑力的影响。

对于准同一Hertz稳态滚动接触问题，这里准同一是指两个接触体具有相同的材料常数，在受碾压过程中，可以忽略接触斑切向力分布对法向位移差的影响，也可以忽略正压力分布对切向变形的影响。Kalker在研究中假设轮轨接触区域为全黏着状态，切向力以及由它得出的合力和旋转力矩都是蠕滑率和自旋蠕滑率的线性函数，这也是它被称为Kalker线性蠕滑理论的原因。

1973年，Kalker借助于线性理论模型法发展了一种快速计算模型－简化理论。该理论假设弹性体与坚硬地基相固结为一薄层，在接触区中任意一点弹性位移仅和作用在该点力有关，且某方向的位移仅和其同方向的力有关。该理论的特点是在理论上比较简单，其配套程序FASTSIM计算速度快，因此适用于车辆运动的分析，是深受车辆动力学研究人员欢迎的轮轨力模型之一。但其计算误差因条件而异，最大可能达到15%左右1。