[科普中国]-守恒型方程

简介

在经典力学范畴内，任何流体运动的规律都是由以下牛顿三个基本定律为基础的：(1)质量守恒定律；(2)牛顿第二定律：动量定理；(3)能量守恒定律。这三个基本定律可由积分/微分形式的数学方程组来描述。计算流体力学(CFD,Computationnal Fliud Dynamics)的核心任务就是通过数值离散方法把这些方程求解出来，从而得到流场在离散的时间/空间点上的数值解。

我们首先在流场中划分一个有限大小的空间，这个空间是虚构的，存在以下两种情况：

①这个空间是固定的。当流体穿越虚构的空间界面时，我们对这个体积内的流体进行数学描述，得到的方程就是守恒型的方程。这里假设的空间大小是有 限体积，包含了许多流体微团，称得到的方程为积分形式的守恒型方程。如果空间缩小为流体微团大小，称得到的方程为微分形式的守恒型方程。

②这个空间随流体一起运动。流体不能穿越这个虚构空间的界面，空间内的流体微团不能与外界交换。此时微团的性质随空间位置的不同而不同，虚构空间的体积也会发生变化。同上，对于有限体积，得到积分形式的非守恒型方程，对于流体微团，得到微分形式的非守恒型方程。

流体运动的守恒型方程连续性方程

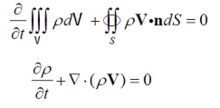
动量方程

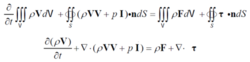
能量方程

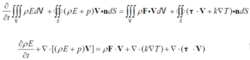
微分方程可由积分型方程在考虑到控制体的形状的任意性后导出。上面的积分方程是在控制体在空间固定的特殊情况下得到的Euler型积分方程。Euler型积分方程直观地反映了质量、动量的守恒关系，也称为守恒型积分方程。对守恒型积分方程直接应用Gauss定理，并考虑到控制体形状的任意性后得到的微分型方程称为守恒型微分方程。