简介
形如y'+P(x)=Q(x)y的微分方程,称为伯努利微分方程,其中n≠0并且n≠11,其中P(x),Q(x)为已知函数,因为当n=0,1时该方程是线性微分方程。它以雅各布·伯努利(Jacob Bernoulli)命名,他在1695年进行了研究。伯努利方程是特殊的,因为它们是具有已知精确解的非线性微分方程。 伯努利方程的着名特殊情况是逻辑微分方程。
转换为线性微分方程伯努利微分方程可以把变量替换成为线性微分方程,将伯努利微分方程两端除以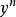 ,得
,得
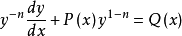
作变量替换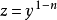 ,则
,则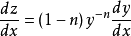 。代入上式,有:
。代入上式,有:
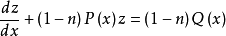
这是以z为未知函数的一阶线性微分方程,由此方程解出z,再由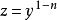 可得伯努利微分方程的解。2
可得伯努利微分方程的解。2
注意,对于n=0和n = 1,伯努利方程是线性的。 对于n≠0和n≠1,替换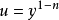 将任何伯努利方程调整到线性微分方程。 例如:
将任何伯努利方程调整到线性微分方程。 例如:
让我们考虑以下微分方程:
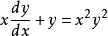
以伯努利形式(用n = 2))重写它:
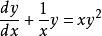
现在,用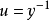 我们得到:
我们得到:
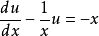 ,它是一个线性微分方程。
,它是一个线性微分方程。
求解
作为线性微分方程的解:
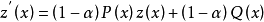
那么我们有
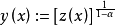
是下面方程的解
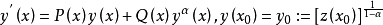
对于每个这样的微分方程,都有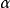 >0,我们有y恒等于0。3
>0,我们有y恒等于0。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国