[科普中国]-充分必要条件

说明

假设A是条件，B是结论

（1）由A可以推出B，由B可以推出A，则A是B的充分必要条件(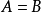 )，或者说A的充分必要条件是B。

（2）由A可以推出B，由B不可以推出A，则A是B的充分不必要条件( )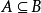

（3）由A不可以推出B，由B可以推出A，则A是B的必要不充分条件( )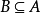

（4）由A不可以推出B，由B不可以推出A，则A是B的既不充分也不必要条件( )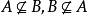

举例1. A=“三角形等边”；B=“三角形等角”。

2. A=“某人触犯了法律”；B=“应当依照刑法对他处以刑罚”。

3. A=“付了足够的钱”；B=“能买到商店里的东西”。

例1中A是B的充分必要条件；

例2中A是B的必要不充分条件；（A触犯法律包含各种法，有刑法有民法；B已经确定是刑法。B属于A所以A是B的必要不充分条件）

例3中A是B的充分必要条件。

生活中生活中表达充分必要条件的情况不太常见。在逻辑学和数学中一般用“当且仅当”来表示充分必要条件。例如：

当且仅当竞争对手甲退出投标时，乙才会报一个较高的价位。

a、b为任意实数时，a²+b² ≥ 2ab 成立，当且仅当a=b时取等号。

其他常见的表示充分必要条件的说法还有：“需要且只需要”、“唯一条件”的情况。例如：

任何两个端节点之间的转发需要且只需要经过三次交换。

为了防止圆管内流动的水发生结冰，则需要且只需要保持圆管内壁面的最低温度在某一温度以上。

俄军逼近格首都称停火唯一条件是格军放弃武力。

逻辑学中定义：如果有事物情况A，则必然有事物情况B；如果没有事物情况A，则必然没有事物情况B，A就是B的充分必要条件。

充分必要条件是逻辑学在研究假言命题及假言推理时引出的。1

陈述某一事物情况是另一件事物情况的充分必要条件的假言命题叫做充分必要条件假言命题。充分必要条件假言命题的一般形式是：p当且仅当q。符号为：p←→q(读作“p等值q”) 。例如“三角形等边当且仅当三角形等角。”是一个充分必要条件假言命题。

根据充分必要条件假言命题的逻辑性质进行的推理叫充分必要条件假言推理。

数学中有命题p、q，如果p推出q且q推出p，则p是q的充分必要条件，简称充要条件。2

p推出q，p是q的充分条件，同时q是p的必要条件，此时p是q的子集。

例如：a、b一正一负推出ab