起源
2000多年前,古希腊数学家最先开始研究圆锥曲线123,并获得了大量的成果。古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究这几种曲线。用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;用平行于圆锥的轴的平面截取,可得到双曲线的一支(把圆锥面换成相应的二次锥面时,则可得到双曲线)。阿波罗尼曾把椭圆叫“亏曲线”,把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”。事实上,阿波罗尼在其著作中使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果。
定义几何观点用一个平面去截一个二次锥面,得到的交线就称为圆锥曲线(conic sections)。
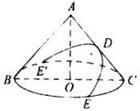
通常提到的圆锥曲线包括椭圆,双曲线和抛物线,但严格来讲,它还包括一些退化情形。具体而言:
1) 当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。
2) 当平面与二次锥面的母线平行,且过圆锥顶点,结果退化为一条直线。
3) 当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
4) 当平面只与二次锥面一侧相交,且不过圆锥顶点,并与圆锥的对称轴垂直,结果为圆。
5) 当平面只与二次锥面一侧相交,且过圆锥顶点,结果为一点。
6) 当平面与二次锥面两侧都相交,且不过圆锥顶点,结果为双曲线(每一支为此二次锥面中的一个圆锥面与平面的交线)。
7) 当平面与二次锥面两侧都相交,且过圆锥顶点,结果为两条相交直线。
注意,上述曲线类中不含有二次曲线:两平行直线。
代数观点在笛卡尔平面上,二元二次方程 的图像称为二次曲线。根据判别式的不同,包含了椭圆、双曲线、抛物线以及各种退化情形。
的图像称为二次曲线。根据判别式的不同,包含了椭圆、双曲线、抛物线以及各种退化情形。
焦点--准线及其推广观点传统的焦点-准线统一定义
(许多年来沿用的焦点--准线观点只能定义圆锥曲线的主要情形,因而不能算是圆锥曲线的定义。但因其形式简明美观,并能引导出许多圆锥曲线中重要的几何概念和性质,而受青睐并广泛运用。)
给定一点P,一直线L以及一非负实常数e,则到P的距离与L距离之比为e的点的轨迹是圆锥曲线。
根据e的范围不同,曲线也各不相同。具体如下:
1) e=0,轨迹为一点或一个圆;
2) e=1(即到P与到L距离相同),轨迹为抛物线;
3) 01,e|t|1,e|t|PL,矩形PSRV超出矩形PLJV;而抛物线,短形PLJV恰好填满。故而,椭圆、双曲线、抛物线的原名分别叫“亏曲线”、“超曲线”和“齐曲线”。这就是阿波罗尼引入的圆锥曲线的定义。
阿波罗尼所给出的两个结论,也很容易用现代数学符号来表示:
趋向无穷大时,LS=0,即抛物线,亦即椭圆或双曲线的极限形式。
在阿波罗尼的《圆锥曲线》问世后的13个世纪里,整个数学界对圆锥曲线的研究一直没有什么新进展。11世纪,阿拉伯数学家曾利用圆锥曲线来解三次代数方程,12世纪起,圆锥曲线经阿拉伯传入欧洲,但当时对圆锥曲线的研究仍然没有突破。直到16世纪,有两件事促使了人们对圆锥曲线作进一步研究。一是德国天文学家开普勒(Kepler,1571~1630)继承了哥白尼的日心说,揭示出行星按椭圆轨道环绕太阳运行的事实;二是意大利物理学家伽利略(Galileo,1564~1642)得出物体斜抛运动的轨道是抛物线。人们发现圆锥曲线不仅是依附在圆锥面上的静态曲线,而且是自然界物体运动的普遍形式。于是,对圆锥曲线的处理方法开始有了一些小变动。譬如,1579年蒙蒂(Guidobaldo del Monte,1545~1607)椭圆定义为:到两个焦点距离之和为定长的动点的轨迹。从而改变了过去对圆锥曲线的定义。不过,这对圆锥曲线性质的研究推进并不大,也没有提出更多新的定理或新的证明方法。
17世纪初,在当时关于一个数学对象能从一个形状连续地变到另一形状的新思想的影响下,开普勒对圆锥曲线的性质作了新的阐述。他发现了圆锥曲线的焦点和离心率,并指出抛物线还有一个在无穷远处的焦点,直线是圆心在无穷远处的圆。从而他第一个掌握了这样的事实:椭圆、抛物线、双曲线、圆以及由两条直线组成的退化圆锥曲线,都可以从其中一个连续地变为另一个,只须考虑焦点的各种移动方式。譬如,椭圆有两个焦点F1、F2,如图4,若左焦点F1固定,考虑F2的移动,当F2向左移动,椭圆逐渐趋向于圆,F1与F2重合时即为圆;当F2向右移动,椭圆逐渐趋向于抛物线,F2到无穷远处时即为抛物线;当F2从无穷远处由左边回到圆锥曲线的轴上来,即为双曲线;当F2继续向右移动,F2又与F1重合时即为两相交直线,亦即退化的圆锥曲线。这为圆锥曲线现代的统一定义提供了一个合乎逻辑的直观基础。
随着射影几何的创始,原本为画家提供帮助的投射、截影的方法,可能由于它与锥面有着天然的联系,也被用于圆锥曲线的研究。在这方面法国的三位数学家笛沙格(Desargue1591-1661)、帕斯卡(Pascal,1623-1662)和拉伊尔(Phailippe de La Hire,1640~1718)得出了一些关于圆锥曲线的特殊的定理,可谓别开生面。而当法国另外两位数学家笛卡儿和费马创立了解析几何,人们对圆锥曲线的认识进入了一个新阶段,对圆锥曲线的研究方法既不同于阿波罗尼,又不同于投射和截影法,而是朝着解析法的方向发展,即通过建立坐标系,得到圆锥曲线的方程,进而利用方程来研究圆锥曲线,以期摆脱几何直观而达到抽象化的目标,也可求得对圆锥曲线研究高度的概括和统一。
到18世纪,人们广泛地探讨了解析几何,除直角坐标系之外又建立极坐标系,并能把这两种坐标系相互转换。在这种情况下表示圆锥曲线的二次方程也被化为几种标准形式,或者引进曲线的参数方程。1745年欧拉发表了《分析引论》,这是解析几何发展史上的一部重要著作,也是圆锥曲线研究的经典之作。在这部著作中,欧拉给出了现代形式下圆锥曲线的系统阐述,从一般二次方程出发,圆锥曲线的各种情形,经过适当的坐标变换,总可以化以下标准形式之一:
继欧拉之后,三维解析几何也蓬勃地发展起来,由圆锥曲线导出了许多重要的曲面,诸如圆柱面、椭球面、单叶和双叶双曲面以及各种抛物面等。
总而言之,圆锥曲线无论在数学以及其他科学技术领域,还是在我们的实际生活中都占有重要的地位,人们对它的研究也不断深化,其研究成果又广泛地得到应用。这正好反映了人们认识事物的目的和规律。
在此,要提到的是我国数学教师胡新平在2016年给出的新成果,千百年来,平面解析几何的主要理论一直再无大的进展,即使焦点—准线系统统一性从公元300多年Pappus首次发现至今已1700年了,其存在的明显不足也一直没能得到完善。事实上,人们也一直在寻求以几何方式统一七类二次曲线,而胡新平老师给出了包含一、二次曲线全部八类曲线的几何统一形式,该统一是焦点-准线下统一性的推广,也是仅见到的完备的、几何形式的统一,这使得平面解析几何向前迈出了里程碑的一步。也是我国数学工作者在平面解析几何学科发展史上留下的深深印记。
性质一、二次曲线的统一方程和性质可以参看《数学通报》2016,12期《一、二次曲线的轨迹统一及性质》一文。
椭圆文字语言定义:平面内一个动点到一个定点与一条定直线的距离之比是一个小于1的正常数e。平面内一个动点到两个定点(焦点)的距离和等于定长2a的点的集合(设动点为P,两个定点为F1和F2,则PF1+PF2=2a)。定点是椭圆的焦点,定直线是椭圆的准线,常数e是椭圆的离心率。
标准方程:
1、中心在原点,焦点在x轴上的椭圆标准方程: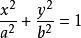
其中 ,
,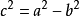 。
。
2、中心在原点,焦点在y轴上的椭圆标准方程: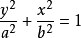
其中 ,
,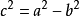 。
。
参数方程: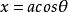 ;
;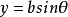 (θ为参数,0≤θ≤2π)
(θ为参数,0≤θ≤2π)
双曲线(的一支)文字语言定义:平面内一个动点到一个定点与一条定直线的距离之比是一个大于1的常数e;平面内一个动点到两个定点(焦点)的距离差等于定长2a的点的集合(设动点为P,两个定点为F1和F2,则│PF1-PF2│=2a)定点是双曲线的焦点,定直线是双曲线的准线,常数e是双曲线的离心率。
标准方程:
1、中心在原点,焦点在x轴上的双曲线标准方程: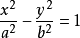
其中a>0,b>0,c²=a²+b².
2、中心在原点,焦点在y轴上的双曲线标准方程: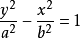
其中a>0,b>0,c²=a²+b².
参数方程:x=asecθ;y=btanθ (θ为参数 )
抛物线文字语言定义:平面内一个动点到一个定点与一条定直线的距离之比是等于1。定点是抛物线的焦点,定直线是抛物线的准线。
参数方程
x=2pt² y=2pt (t为参数) t=1/tanθ(tanθ为曲线上点与坐标原点确定直线的斜率)特别地,t可等于0
直角坐标
y=ax²+bx+c (开口方向为y轴,a≠0) x=ay²+by+c (开口方向为x轴,a≠0 )
离心率椭圆,双曲线,抛物线这些圆锥曲线有统一的定义:平面上,到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。且当0PF2)
|PF2|=a-ex(PF2b>0)
x²/a²-y²/b²=1 (a>0,b>0)
y²=2px (p>0)
中点弦问题已知圆锥曲线内一点为圆锥曲线的一弦中点,求该弦的方程:
1、联立方程法。
用点斜式设出该弦的方程(斜率不存在的情况需要另外考虑),与圆锥曲线方程联立求得关于x的一元二次方程和关于y的一元二次方程,由韦达定理得到两根之和的表达式,再由中点坐标公式和两根之和的具体数值,求出该弦的方程。
2、点差法(代点相减法)
设出弦的两端点坐标(x₁,y₁)和(x₂,y₂),代入圆锥曲线的方程,将得到的两个方程相减,运用平方差公式得[(x₁+x₂)(x₁-x₂)]/a²+[(y₁+y₂)(y₁-y₂)/b²]=0
由斜率为(y₁-y₂)/(x₁-x₂),可以得到斜率的取值(使用时注意判别式的问题)
统一方程平面直角坐标系内的任意圆锥曲线可用如下方程表示:
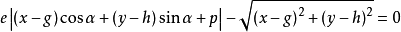
其中,α∈[0,2π),p>0,e≥0。
①e=1时,表示以F(g,h)为焦点,p为焦点到准线距离的抛物线。其中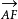 与极轴夹角α(A为抛物线顶点)。
与极轴夹角α(A为抛物线顶点)。
②00
Δ=0
有一实点的相交虚直线




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国