[科普中国]-平行四边形

定义

两组对边分别平行的四边形叫做平行四边形1。

1.平行四边形属于平面图形。

2.平行四边形属于四边形。

3.平行四边形属于中心对称图形。

性质（矩形、菱形、正方形都是特殊的平行四边形。）

（1）如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。

（简述为“平行四边形的两组对边分别相等”2）

（2）如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等。

（简述为“平行四边形的两组对角分别相等”2）

（3）如果一个四边形是平行四边形，那么这个四边形的邻角互补。

（简述为“平行四边形的邻角互补”）

（4）夹在两条平行线间的平行的高相等。（简述为“平行线间的高距离处处相等”）

（5）如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分。

（简述为“平行四边形的对角线互相平分”2）

（6）连接任意四边形各边的中点所得图形是平行四边形。（推论）

（7）平行四边形的面积等于底和高的积。（可视为矩形。）

（8）过平行四边形对角线交点的直线，将平行四边形分成全等的两部分图形。

（9）平行四边形是中心对称图形，对称中心是两对角线的交点.

（10）平行四边形不是轴对称图形，但平行四边形是中心对称图形。矩形和菱形是轴对称图形。注：正方形，矩形以及菱形也是一种特殊的平行四边形，三者具有平行四边形的性质。

（11）平行四边形ABCD中（如图）E为AB的中点，则AC和DE互相三等分，一般地，若E为AB上靠近A的n等分点，则AC和DE互相(n+1)等分。

（12）平行四边形ABCD中，AC、BD是平行四边形ABCD的对角线，则各四边的平方和等于对角线的平方和。

（13）平行四边形对角线把平行四边形面积分成四等份。

（14）平行四边形中，两条在不同对边上的高所组成的夹角，较小的角等于平行四边形中较小的角，较大的角等于平行四边形中较大的角。

（15）平行四边形的面积等于相邻两边与其夹角正弦的乘积3

其他性质平行四边形的对边是平行的（根据定义），因此永远不会相交。

平行四边形的面积是由其对角线之一创建的三角形的面积的两倍。

平行四边形的面积也等于两个相邻边的矢量交叉乘积的大小。

任何通过平行四边形中点的线将该区域平分。

任何非简并仿射变换都采用平行四边形的平行四边形。

平行四边形具有2阶（至180°）的旋转对称性（如果是正方形则为4阶）。如果它也具有两行反射对称性，那么它必须是菱形或长方形（非矩形矩形）。如果它有四行反射对称，它是一个正方形。

平行四边形的周长为2（a + b），其中a和b为相邻边的长度。

与任何其他凸多边形不同，平行四边形不能刻在任何小于其面积的两倍的三角形。

在平行四边形的内侧或外部构造的四个正方形的中心是正方形的顶点。

如果与平行四边形平行的两条线与对角线并行构成，则在该对角线的相对侧上形成的平行四边形面积相等[7]

平行四边形的对角线将其分成四个相等面积的三角形。

判定两组对边分别平行的四边形是平行四边形（定义判定法）；

一组对边平行且相等的四边形是平行四边形；

两组对边分别相等的四边形是平行四边形；

两组对角分别相等的四边形是平行四边形（两组对边平行判定）；

对角线互相平分的四边形是平行四边形。

补充：条件3仅在平面四边形时成立，如果不是平面四边形，即使是两组对边分别相等的四边形，也不是平行四边形。

辅助线一、连接对角线或平移对角线。4

二、过顶点作对边的垂线构成直角三角形。

三、连接对角线交点与一边中点，或过对角线交点作一边的平行线，构成线段平行或中位线。

四、连接顶点与对边上一点的线段或延长这条线段，构造相似三角形或等积三角形。

五、过顶点作对角线的垂线，构成线段平行或三角形全等。

相关计算1、（1）平行四边形的面积公式：底×高（可运用割补法，推导方法如图）；如用“h”表示高，“a”表示底，“S”表示平行四边形面积，则S平行四边形=a*h。4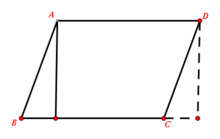

（2）平行四边形的面积等于两组邻边的积乘以夹角的正弦值；如用“a”“b”表示两组邻边长，α表示两边的夹角，“S”表示平行四边形的面积，则S平行四边形=ab*sinα。

2、平行四边形周长：四边之和。可以二乘（底1+底2）；如用“a”表示底1，“b”表示底2，“c平”表示平行四边形周长，则平行四边的周长c=2(a+b)。5

特殊的平行四边形矩形定义：有一个角是直角的平行四边形是矩形。

判定：

1.有一个角是直角的平行四边形是矩形；

2.对角线相等的平行四边形是矩形；

3.有三个角是直角的四边形是矩形；

4.对角线相等且互相平分的四边形是矩形。

性质：

1.矩形具有平行四边形的一切性质；

2.矩形的对角线相等；

3.矩形的四个角都是90度；

4.矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点。

菱形定义：有一组邻边相等的平行四边形是菱形。

判定：

1.一组邻边相等的平行四边形是菱形；

2.对角线互相垂直的平行四边形是菱形；

3.四边相等的四边形是菱形。

性质：

1.菱形具有平行四边形的一切性质；

2.菱形四边相等；

3.菱形每条对角线平分一组对角；

4.菱形是中心对称图形，也是轴对称图形。

正方形定义：一组邻边相等且有一个角是直角的平行四边形是正方形。

判定：

1.一组邻边相等的矩形是正方形；

2.有一个角是直角的菱形是正方形；

3.对角线互相垂直的矩形是正方形；

4.对角线相等的菱形是正方形。

性质：

正方形具有矩形和菱形的一切性质。6

例题1．用边长分别为50cm，75cm，100cm的两个全等三角形拼成四边形，共能拼成_________个四边形，___________个为平行四边形。

2．在四边形ABCD中，若AB=CD，再添加一个条件为__________，就可以判定四边形ABCD为平行四边形。

3．延长△ABC的中线AD至E，使DE=AD，连接BE，CE，则AB_________CE，AC_________BE。

4．若四边形ABCD中，AC，BD相交于点O，要判定它为平行四边形，从角的关系看应满足____对角相等_______，从对角线的关系看应满足______对角线互相平分_________。

5．已知E、F、G、H分别为ABCD各边的中点，则四边形EFGH为_______________。

二、选一选

6．能识别四边形ABCD是平行四边形的题设是（ ）

A．AB∥CD，AD=BC

B．∠A=∠B，∠C=∠D

C．AB=CD，AD=BC

D．AB=AD，CB=CD

7．点A，B，C，D在同一平面内，从①AB∥CD，②AB=CD，③BC∥AD，④BC=AD这四个条件中任选两个，能使四边形ABCD是平行四边形的选法有（）

A．3种 B．4种 C．5种 D．6种

8．下列结论正确的是（ ）

A．对角线相等且一组对角相等的四边形是平行四边形

B．一边长为125cm，两条对角线长分别是100cm和150cm的四边形是平行四边形

C．一组对边平行且一组对角相等的四边形是平行四边形

D．对角线相等的四边形是平行四边形

9．不能判定四边形ABCD是平行四边形的条件是（）

A．AB=CD，AD=BC

B．AB∥CD，AB=CD

C．AB=CD，AD∥BC

D．AB∥CD，AD∥BC

10．如图19－1－26，在ABCD中，E，F分别在BC，AD上，若想使四边形AFCE为平行四边形，须添加一个条件，这个条件可以是（ ）。

①AF=CF；②AE=CF；③∠BAE=∠FCD；④∠BEA=∠FCE。

A．①或② B．②或③ C．③或④ D．①或③或④

11．如图19－1－27，在△ABC中，DE∥AB，FD∥BC，EF∥AC，则下列说法中正确的有（ ）个。

①图中共有三个平行四边形；

②AF=BF，CE=BE，AD=CD；

③EF=DE=DF；

④图中共有三对全等三角形。

A．1 B．2 C．3 D．4

三、解答题

12．如图19－1－28，在ABCD中，E，F为BD上的点，BF=DE，那么四边形AECF是什么图形？试用两种方法证明。

13．已知：在△ABC中，AB=AC，EF是△ABC的中位线，分别交AB，AC于E，F，延长AB到D，使BD=AB，连接CD。求证：。

14．如图19－1－29，ABCD中，对角线AC、BD相交于点O，过点O作两条直线分别与AB，BC，CD，AD交于G，F，H，E四点。求证：四边形EGFH是平行四边形。

15．如图19－1－30，分别以△ABC的三边为边长，在BC的同侧作等边三角形ABD，等边三角形BCE，等边三角形ACF，连接DE，EF。求证：四边形ADEF是平行四边形。

四、思维拓展

16．如图19－1－31，在ABCD中，AE⊥BD，CF⊥BD，垂足分别为点E，F，点G，H分别为AD，BC的中点，试证明EF和GH互相平分。

17．如图19－1－32，△ABC是边长为100px的边三角形，P是△ABC内的任意一点，过点P作EF∥AB分别交AC，BC于点E，F，作GH∥BC分别交AB，AC于点G，H，作MN∥AC分别交AB，BC于点M，N，试猜想：EF+GH+MN的值是多少？其值是否随P位置的改变而变化？并说明你的理由。

五、中考热身

18．（2005年苏州市）如图19－1－33，在ABCD中，下列各式不一定正确的是（ ）。

A．∠1+∠2=180°

B．∠2+∠3=180°

C．∠3+∠4=180°

D．∠2+∠4=180°

答案：

1．六；三。2．AB∥CD或AD=BC。3．= ; =4．∠A=∠C，∠B=∠D，

∠A+∠B=∠B+∠C=∠C+∠D=∠D+∠A=180°；AO=CO，BO=DO5．平行四边形

6．C 7．B 8．C 9．C 10．D 11．B

12．平行四边形。方法一：连接AC，利用“对角线互相平分的四边形为平行四边形”来证明。

方法二：证△ABE≌△CDF， △AFD≌△CEB，利用“两组对边分别相等的四边形为平行四边形”来证明。

13．提示：先证明△EBC≌△FCB，得CE=BF，再证。

14．先证△AEO≌△CFO，得OE=OF，同理可得OG=OH，所以四边形EGFH是平行四边形。

15．先证△EDB≌△CFE，可得BD=EF，ED=CF。∵BD=DA，CF=AF，∴ED=AF，EF=DA，∴四边形ADEF是平行四边形。

16．提示：连接GE，EH，HF，GF，先证GE=HF，再证GE∥HF即可。

17．其值为200px，且不随P位置的改变而变化。

理由：由△ABC为等边三角形可得△AGH也是等边三角形，

∴GH=AG=AM+MG ①，

同理，△BMN也为等边三角形，

∴MN=MB=MG+GB。②

∵MN∥AC，EF∥AB，

∴四边形AMPE为平行四边形，

∴PE=AM，同理，BFPG也为平行四边形，

∴PF=GB，

∴EF=PE+PF=AM+GB。③

①+②+③得EF+GH+MN=AM+GB+MG+GB+AM+MG=2（AM+MG+GB）=2AB=2×4=200px。

18．D