[科普中国]-傅立叶定律

简介

热传导定律也称为傅里叶定律，表明单位时间内通过给定截面的热量，正比例于垂直于该截面方向上的温度变化率和截面面积，而热量传递的方向则与温度升高的方向相反。 我们可以用两种等效的形式来表述这个定律：整体形式以及差分形式。

牛顿的冷却定律是傅立叶定律的离散推广，而欧姆定律则是傅立叶定律的电学推广。2

热传导固体中的热传导是源于晶格振动形式的原子活动（声子）。近代的观点把这种能量传输归因于原子运动导致的晶格波造成的。在非导体中，能量传输只依靠晶格波进行；在导体中（比如 银、铁），除了晶格波还有自由电子的平抑运动。用来衡量不同物体导热能力的物理量就是热导率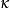 (W·m-1·K-1 )。

数学表达式【英译】：Fourier's Law

【中文】：傅立叶定律

傅立叶定律是传热学中的一个基本定律，由法国著名科学家傅里叶于1822年提出。3

傅里叶定律的文字表述：在导热现象中，单位时间内通过给定截面的热量，正比例于垂直于该截面方向上的温度变化率和截面面积，而热量传递的方向则与温度升高的方向相反。

傅里叶定律用热流密度JT 表示时形式如下：

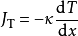
可以用来计算热量的传导量。其中热流密度JT (W·m-2) 是在与传输方向相垂直的单位面积上，在x方向上的传热速率。它与该方向上的温度梯度dT/dx成正比。比例常数κ是一个输运特性，称为热导率（也称为 导热系数），单位是 (W·m-1·K-1)。也可以表述如下：

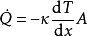
其中 dQ/dt (Q上一点) 为导热速率（或记为IT），单位为W.

A 为传热面积，单位为m2

T 为温度，单位为K

x 为在导热面上的坐标，单位为m

一般形式的数学表达式：

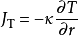
式中：JT 是在r方向上的热流密度，它垂直于等温表面。热流密度是一个向量，也可以将热流密度向量分解为几个分量。

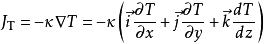
上述式中负号表示传热方向与温度梯度方向相反。4

【物理学类比】热学中的热导率及热流密度可以类比于电学中的电导率和电流密度 J=σE。记 ET=dT/dx 为温度场强度，则热流密度可以写成 JT=-κET。若把温度差的相反数 -ΔT记为温压差 ΔUT，则可以推得 ΔUT=RTIT，该式称为热欧姆定律。其中IT为导热速率（见上方公式），RT 表示热阻，可推得 RT=ρTL/A，该式称为热阻定律，其中ρT=1/κ 为热阻率，热阻也和电阻类似，满足串并联规则。5

关键要点傅立叶定律是热传导的基础。它并不是由热力学第一定律导出的数学表达式，而是基于实验结果的归纳总结，是一个经验公式。同时，傅立叶定律是定义材料的一个关键物性，热导率的一个表达式。

另外，如上所述，傅立叶定律是一个向量表达式。热流密度是垂直于等温面的，并且是沿着温度降低的方向。傅立叶定律适用于所有物质，不管它处于什么状态（固体、液体或者气体）。

热质的运动和传递中的应用物质具有的热能(粒子无规运动动能)是物质能量形式之一，它又对应着物质所具有的热质量，并且可看作为是热子气的质量。物体导热过程中的热量输运对应着热质量(热子气质量)的输运。与对流输运不同，热质的输运是属于分子输运或扩散输运。它可以用热子气的宏观速度(漂移速度)来描述。

描述物体的机械运动，我们需要有物体的质量、运动速度和加速度等物理量以及牛顿运动定律。与此类似，为了能够描述和研究热子气的宏观运动，需要建立热子气运动的速度和加速度等物理量。为了能确定热子气运动状态的变化与施加在热子气之上的非平衡作用力之间的关系，我们需要建立热质运动定律。

傅立叶导热定律是指在具有不均匀温度场的物体中，各点热流密度与其所在处的温度梯度方向相反，数量上成正比，其比例系数为导热系数：

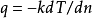
傅立叶导热定律的物理意义通常被理解为：温度梯度是驱动力，热流密度则是被驱动的热量流。在不可逆过程热力学中把前者称之为热力学力，后者称之为热力学流同。在有关输运现象的文献中常把傅立叶导热定律和牛顿粘性定律进行类比。牛顿粘性定律描述的是流体的本构关系，而傅立叶导热定律描述的则是流和温度梯度的关系。

我们基于傅立叶定律以及忽略惯性力的热子气守恒方程，求得了上述热子气粘性力的表达式。与此同时，从式可以看到傅立叶导热定律是反映了热子气压力与粘性力的平衡，是热子气动量方程在忽略惯性力条件下的一种近似。

研究发现：傅立叶导热定律本质上是忽略惯性力条件下的热子气的压力梯度与粘性力的平衡方程；当惯性力可以忽略时，热子气的动量守恒方程退化为傅立叶导热定律。在极低温或极高热流密度时傅立叶导热定律不再适用。