[科普中国]-三次曲线

三次曲线（Cubic Curves）是一条平面代数曲线，显然， 它和一般的直线都相交三个点。

定义它是用三元三次齐次方程在射影平面上的零点集来定义的：F(x,y,z)=0, deg F=3.

一般来说，应用齐次坐标，三次曲线有以下几项组成：

x3,y3,z3,x2y,x2z,y2x,y2z,zx3,z2y,xyz.12即：ax3+bx2y+cxy2+dy3+ex2+fxy+gy2+hx+iy+j= 0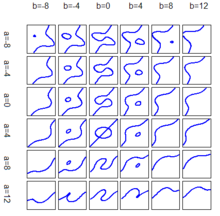

图为4x3- ax2y +9xy2-9y3-36x +36y +10b =0光滑的三次曲线是亏格1曲线， 所以也是椭圆曲线。

发展史在牛顿之前，也没有人能够像把非退化二次曲线分成椭圆、双曲线与抛物线那样对三次曲线分类。牛顿从1664年起试图追随笛卡儿按方程次数对曲线分类的思路来解决这一课题。1667—1668年和1678—1679年间，他又两度回到高次曲线的研究并获重大进展。但如其一贯所为，牛顿迟疑于结果的发表，直到1695年，他才将以前的结果总结成专论《三次曲线枚举》(Enumeratio linearum tertii ordinis)并作为《光学》的附录发表(1704)。

Cayley—Bacharach定理两条三次曲线有九个交点。 如果第三条三次曲线经过前两条三次曲线的8个交点， 那么它也必定通过第九个交点。34这就是著名的凯莱-巴拉赫性质**（Cayley–Bacharach theorem）。事实上，这条定理被Chasles先证出，又被Cayley，Bacharach推广到高次形式，因此又称为Chasles定理**。上述性质可以推演出许多射影几何中有关三点共线（或三线共点）的定理， 如帕斯卡定理、帕普斯定理等等，均可简易证出。

特别的，过一个3x3“笼子”（Cages5）中八个点的三次曲线，也过第九个点。（这个定理也被形象的称为三次曲线的“笼子”定理（Cage Theorem for Cubics）。值得一提的是，这个定理与Gorenstein Ring（戈伦斯坦环）有紧密联系。因此虽然一般九点确定可以确定一条三次曲线，但如果九点处于一种特殊的位置，则确定不了一条三次曲线。有关Pappus定理和Pascal定理的证明，可参考： CAYLEY-BACHARACH THEOREMS AND CONJECTURES，D. Eisenbud, M. Green and J. Harris

有关Cayley-Bacharach定理的推广及其他，可参考： CURVES IN CAGES: AN ALGEBRO-GEOMETRIC ZOO，Gabriel Katz

众多的三次曲线引言《三次曲线枚举》首先根据平面曲线与直线相交所产生的交点数来定义曲线的阶，同时指出圆锥曲线的许多概念与性质可以被推广至高次曲线．例如牛顿提出了适合高次曲线的一般直径理论(在这理论中n次曲线的直径被定义为该曲线与一平行直线簇中每一条的n个交点的重心轨迹)和一般渐近线理论等。

Newton讨论了三次曲线的分类．他注意到任一三次曲线至少有一个实渐近方向，取与此方向平行的直线为坐标轴之一，牛顿导出了三次曲线方程的四类基本形式——事实上：Newton发现他们都是五种三次发散抛物线（Newton如是说，即divergent cubic parabolas）的投影，正像所有的圆锥曲线都可看作是圆的投影一样——由此Newton将所有三次曲线分为72类，而丢失了其中的六类（J．斯特林(Stirling，1717)、G．克莱姆(Cramer，1746)等人又追加了6种)。Newton的分类方法被欧拉批评，被认为缺乏一般性——不过这是后话。Plücker后来又改了更完善的219种分类。

在仿射平面上，每个三次曲线与无穷远线有三个交点，必有一实交点（另外两个也可以是实交点，也可以是共轭的虚交点）。交点处的切线即为渐近线，这样我们必得到一个实渐近线，并以此为轴，可化简为

(i)xy2+ey=ax3+bx2+cx+d，

(ii)xy=ax3+bx2+cx+d，

(iii)y2=ax3+bx2+cx+d，

(iv)y=ax3+bx2+cx+d．

第一类(i)xy2+ey=ax3+bx2+cx+d（立方双曲线） 这也是 最复杂的一类，两边同时乘以x，得

（xy+e/2)2=ax3+bx2+cx+d+1/4*e2（2）

讨论这两个方程的根

其中，比较著名的有蛇形线（Serpentine Curve）：

x2y+a2 y-b2x=0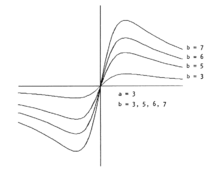**Fig1.**一般立方双曲线

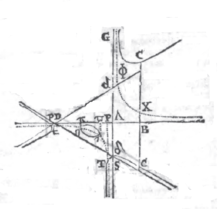一般立方双曲线有三条渐近线，近似于双曲线。中间为卵形线（oval）（三个分支，一内一外，另一个则在两渐近线同侧）且（2）中四实根互异

Fig2-8如右图册所示