[科普中国]-散布图

定义

散布图是用非数学的方式来辨认某现象的测量值与可能原因因素之间的关系。这种图示方式具有快捷，易于交流，和易于理解的特点。用来绘制散布图的数据必须是成对的(X,Y)。通常用垂直轴表示现象测量值Y，用水平轴表示可能有关系的原因因素X。推荐两轴的交点采用两个数据集(现象测量值集，原因因素集)的平均值。收集现象测量值时要排除其他可能影响该现象的因素。例如，测量机器制产品的表面品质时，也要考虑到其它可能影响表面品质的因素，如进给速度、刀具状态等。

散布图又叫相关图，它是将两个可能相关的变数资料用点画在坐标图上，用成对的资料之间是否有相关性。这种成对的资料或许是特性一原因，特性一特性一原因的关系。通过对其观察分析，来判断两个变数之间的相关关系。这种生产中也是常见的，例如热处理时淬火温度与工件硬度之间的关系，某种元素在材料中的含量与材料强度的关系等。这种关系虽然存在，但又难以用精确的公式或函示，在这种情况下用相关图来分析就是很方便的。假定有一对变数x 和y,x影响因素，y 表示某一质量特征值，通过实验或收集到的x 和y 的资料，上用点表示出来，根据点的分布特点，就可以判断x和y 的相关情况。在我们的生活及工作中，许多现象和原因，有些呈规则的关连，有些呈不规则连。我们要了解它，就可借助散布图统计手法来判断它们之间的相关关系。1

作法1、收集X与Y两个变量足够之对应数据。

2、计算X变量测定值的平均值，计算Y变量测定值的平均值。

3、在直角横坐标X轴上划出X值的刻度(刻度在轴的内侧，数字标示在轴的外侧)，并且以最小值当起点，刻度间表示均为同等值。纵坐标Y轴上划出Y值的刻度(刻度在轴的内侧）。

4、X轴与Y轴之交点处不可标示0数字，并且X轴的全宽度与Y轴的全宽度最好相等。

5、将各组之数据的点绘于坐标上：

(1)如有2点重复时以⊙表示。

(2)如有3点重复时以⊙表示。

分类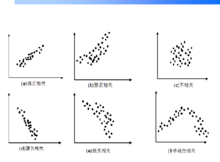1.强正相关（如容量和附料重量）r=+1

2.强负相关（油的粘度与温度） r=-1
3.弱正相关（身高和体重） 0