[科普中国]-样本均值

样本

样本（sample），是指从总体中抽出的一部分个体。样本中所包含个体数目称样本容量或含量，用符号N或n表示。

总体（population）是指客观存在的，并在同一性质的基础上结合起来的许多个别单位的整体，即具有某一特性的一类事物的全体，又叫母体或全域。简单地说，总体也就是我们所研究的性质相同个体的总和。

样本是受审查客体的反映形象或其自身的一部分。按一定方式从总体中抽取的若干个体，用于提供总体的信息及由此对总体作统计推断。又称子样。例如因为人力和物力所限，不能每年对全国的人口进行普查，但可以通过抽样调查的方式来得到需要的信息。从总体中抽取样本的过程叫抽样。最常用的抽样方式是简单随机抽样，按这种方式抽样，总体中每个个体都有同等的机会被抽入样本，这样得到的样本称简单随机样本。样本的平均值称样本均值，样本偏离样本均值的平方的平均值称为样本方差，在数理统计中，常常用样本均值来估计总体均值，用样本方差来估计总体方差。

均值均值是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。在统计工作中，平均数（均值）和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。

均值是统计中的一个重要概念。在统计中算术平均数常用于表示统计对象的一般水平，它是描述数据集中位置的一个统计量。既可以用它来反映一组数据的一般情况、和平均水平，也可以用它进行不同组数据的比较，以看出组与组之间的差别。用平均数表示一组数据的情况，有直观、简明的特点，所以在日常生活中经常用到，如平均速度、平均身高、平均产量、平均成绩等等。

样本均值随机加权多传感器数据融合是近年来发展起来的一种数据处理新技术，对数据融合方法的研究已受到人们的普遍关注。文中首先将一种新兴的随机加权估计方法应用于多传感器数据融合，提出了一种将多源信息综合处理的随机加权数据融合方法。该方法依据极大似然原理，将来自不同总体(均值相同，方差不同)的随机样本进行有效融合，得到新的总体均值估计量，从而消除了低精度检测结果的干扰，提高了综合检测结果的精度。其次，提出了一种基于随机加权估计的多维位置数据最优融合算法。该算法用随机加权估计对每个传感器测得的位置参数进行估计，用最优信息融合算法将这些估计进行融合，得到多传感器系统多维位置参数的最优估计。与其它融合算法相比较，随机加权方法有许多优点如该估计值是无偏的，其估计误差比传统信息融合误差小，且不需要知道参数的精确分布，易于计算。

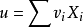
式为估计总体的随机加权数据融合，当所采用的检测方法精度高时权值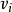大，当所采用的检测方法精度低时权值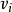小，这样便可消除低精度检测结果的干扰，从而提高综合检测结果的精度。1

样本均值的抽样分布样本均值的抽样分布是所有的样本均值形成的分布，即μ的概率分布。样本均值的抽样分布在形状上却是对称的。随着样本量n的增大，不论原来的总体是否服从正态分布，样本均值的抽样分布都将趋于正态分布，其分布的数学期望为总体均值μ，方差为总体方差的1/n。这就是中心极限定理（central limit theorem）。2

设总体共有N个元素，从中随机抽取一个容量为n的样本，在重置抽样时，共有N·n 种抽法，即可以组成N·n不同的样本，在不重复抽样时，共有N·n个可能的样本。每一个样本都可以计算出一个均值，这些所有可能的抽样均值形成的分布就是样本均值的分布。但现实中不可能将所有的样本都抽取出来，因此，样本均值的概率分布实际上是一种理论分布。

正态总体的样本均值的分布设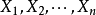是来自正态总体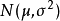的样本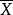，是样本均值，则有3