[科普中国]-样本平均数

简介

样本平均数是从一个或多个随机变量上的数据集合（样本）计算的统计量。样本平均值是总体平均值的估计量，其中总体是指采集样本的集合。

样本平均数是一个向量，每个元素是随机变量之一的样本均值，即每个元素是其中一个变量的观察值的算术平均值。如果仅观察到一个变量，则样本平均数是单个数字（该变量的观察值的算术平均值）。

由于其易于计算和其他期望的特征，样本平均数广泛用于统计和应用中，以表示分布的位置。1

计算方法设xij是第j个随机变量（j = 1，...，K）的第i个独立观察值（i = 1，...，N）。 这些观察结果可以排列成N列向量，每个都有K个子项，K×1列向量给出所有变量的第i个观察值，表示为xi（i = 1，...，N）。

样本平均数向量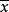是一个列向量，它的第j个元素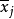是第j个变量的N个观察值的平均值2：

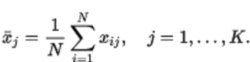
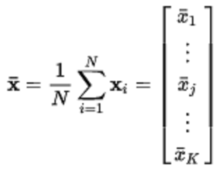
因此，样本平均数包含每个变量的观察值的平均值，并被写入

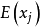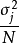样本平均数的差异对于每个随机变量，样本平均数是人口平均值的一个很好的估计量，其中“良好”估计量被定义为有效和无偏差。 当然，由于从同一分布中抽取的不同样本将给出不同的样本平均数，因此对真实均值的估计不同，估计量可能不是群体平均值的真实值。 因此，样本平均数是随机变量，而不是常数，因此具有其自身的分布。 对于第j个随机变量的N个观察值的随机抽样，样本均值的分布本身具有等于群体平均值和方差等于，其中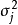是随机变量Xj的方差。3

相关知识如果求出的平均数是由所研究对象全部数据求出的，就叫做总体平均数；如果是由样本求出的，就叫做样本平均数。可以用样本平均数去估算总体平均数.

计算方法：（1）若 ， ，…， ，则 (a—常数， ， ，…，接近较整的常数a)；

（2）加权平均数：

（3）平均数是刻划数据的集中趋势(集中位置)的特征数。

通常用样本平均数去估计总体平均数，样本容量越大，估计越准确。