[科普中国]-抛物柱面函数

简介

在数学中，抛物柱面函数是作为微分方程解的一类特殊函数。

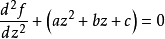
当在抛物柱面坐标中表示时，在拉普拉斯方程上使用变量分离技术时，发现了该方程。

通过完成称为H. F.韦伯方程（Weber 1869）的平方和重新缩放z，可以将上述方程式分成两种不同的形式（A）和（B））：

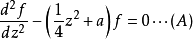
如果f（a,z）是解，那么f（a,-z）、f（-a,iz）、f（-a,-iz）也都是解。

如果f（a,z）是方程（A）的解，那么f（-ia,ze(1/4)πi）是方程（B）的解，并且类似的，f（-ia,-ze(1/4)πi）、f（ia,-ze-(1/4)πi）、f（ia,ze-(1/4)πi）也是方程（B）的解。123

求解有（A）形式的独立偶数和奇数解。 这些是由（阿布拉莫维茨和史蒂文（1965年））给出的4：

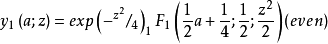
和

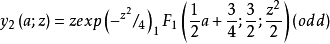
其中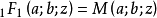是超几何函数。

可以由上述解的线性组合形成其他成对的独立解。 这样的组合是基于他们在无穷远的函数：

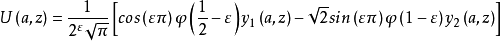
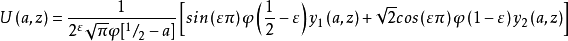
这里，。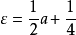

当| arg（z）|