[科普中国]-序关系

简介

偏序关系，亦称序关系、弱偏序关系、半序关系，是一种重要的二元关系。指集合A有自反性、反对称性和传递性的二元关系R，A称为偏序集。偏序关系常用记号≤表示（仍读作小于或等于）。a≤b意即aRb。偏序关系可用符号表示为：R是A的偏序关系。。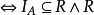

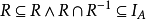定义1，设P是集合，P上的二元关系“≤”满足以下三个条件，则称“≤”是P上的偏序关系（或部分序关系）：

（1）自反性：a≤a，∀a∈P；

（2）反对称性：∀a，b∈P，若a≤b且b≤a，则a=b；

（3）传递性：∀a，b，c∈P，若a≤b且b≤c，则a≤c；1

特点偏序关系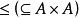有下列特点：

1、对角集；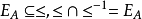

2、≤ 的矩阵(rij)λ的主对角线上的元素全是1；当 i ≠ j 时，rij·rji = 0，当 rij = rjk = 1时，rik=1；

3、≤ 的箭头图上每一点有一箭头从自己出发而指向自己。如有箭头从a指向b，从b指向c，就有箭头从a指向c，任何两点间无双箭头。

偏序关系的逆关系≥一定是偏序关系，偏序关系一定是拟序关系。1880年，皮尔斯（Perice，C.S.）首先系统地讨论了偏序关系，而关于偏序的术语是由豪斯多夫（Hausdorff，F.）从1914年引进的。1

拟序关系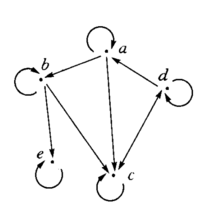也叫做伪序关系或前序关系，一种重要的二元关系。指集合A上的自反的与传递的二元关系R，A称为拟续集，即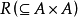关系是拟序关系。。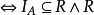

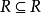拟序关系有下列特点：

1、对角集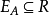，且当∈R，∈R时，∈R。

2、R的矩阵(rij)λ的主对角线上的元素全是1，且当 rij= rjk= 1时，rik=1；

3、R的箭头图上，每个元素有一个从自己出发又指向自身的箭头，且在有a到b的箭头，b到c的箭头时，就有a到c的箭头，如右图的关系箭头表示的是集A={a,b,c,d,e}上的一个拟序。

拟序关系的逆关系一定是拟序的，反对称的拟序关系是偏序关系，但拟序关系可以不是偏序关系。例如，图中表示的拟序就不是偏序，因为cRd且dRc，但c≠d。1