[科普中国]-单叶双曲面

简介

在几何学中，单叶双曲面（有时称为旋转双曲面或圆形双曲面）是通过围绕其主轴旋转双曲线而产生的表面。 双曲面是可以通过使用方向定标使其变形而从旋转抛物面获得的表面。1

双曲面是二次曲面，其可以被定义为三个变量中的二维多项式的点的集合的表面。 在二次曲面中，双曲面的特征在于不仅具有对称中心，而且让平面和其相交还能形成锥体、柱体等。 双曲面还具有三对垂直对称轴和三对垂直对称平面。

给定双曲面，如果选择轴为双曲面对称轴的笛卡尔坐标系，并且原点是双曲面的对称中心，则双曲面可以由以下两个方程之一定义：

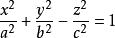
或者

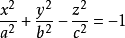
这两个方程均趋近于下面方程的锥。

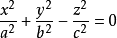
当且仅当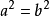 时能形成旋转双曲面。

在第一种情况下（方程式右侧的为1），它是单叶双曲面，也称为双曲面。 它是一个连接表面，每个点都具有负高斯曲率。 这意味着任何点处的切线平面与双曲面相交成两条线，因此单叶双曲面是双重曲面。

在第二种情况（方程式右侧的为-1）中，它具有两片双曲面，也称为椭圆双曲面。 表面有两个连接的部件，每个点都有正高斯曲率。 因此，在这个意义上，表面是凸的，每个点的切线平面仅在这一点上相交。

参数表示可以定义双曲面的笛卡尔坐标，类似于球面坐标，保持方位角θ∈[0,2π），但将倾斜度v变为双曲线三角函数：

单叶双曲面：v∈（-∞，∞）

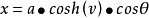
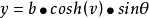
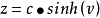
属性表面上的线（1）单叶双曲面包含两根线条。 这是一个双重曲面。

（2）在a = b的情况下，单叶双曲面是旋转表面，可以通过旋转两条线l+或l-，它们偏向旋转轴。x(t)为：

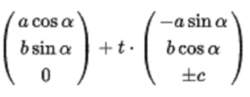
平面部分为了简单起见，设方程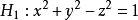 。 因为一般双曲面是单叶双曲面，它的结果也适用于一般情况2。

（1）斜率小于1的平面（1是双曲面上的线的斜率）与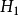 相交形成椭圆；

（2）斜率等于1的平面（包含原点）与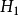 相交形成一对平行线；

（3）斜率等于1的平面（不包含原点）与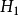 相交形成抛物线；

（4）斜率大于1的非切向平面与 相交形成双曲线。

双曲面的对称性双曲面的方程：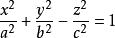

（1）关于原点对称；

（2）关于坐标平面对称；

（3）在a = b（旋转双曲面）的情况下，与z轴旋转对称并对称于包含z轴的任何平面。3

双曲面的曲率单叶双曲面的高斯曲率为负，两片双曲面的高斯曲率为正。 尽管它具有正曲率，但是具有另一适当选择的度量的两张双曲面也可以用作双曲线几何的模型。

应用由于有良好的稳定性和漂亮的外观，单叶双曲面常常应用于一些大型的建筑结构，如发电厂的冷却塔、电视塔等等（见 Hyperboloid structure）。

为迎接2010年亚运会而修建的广州电视塔（高度610m ）的主体结构就是一个典型的单叶双曲面（如图）。4

广州电视塔

火电厂的冷却塔常用的外形之一就是旋转单叶双曲面，它的优点是对流快、散热效果好。（详见）

**英国Didcot发电厂（**Didcot Power Station）的冷却塔（Cooling Tower）