简介
竞赛图是通过在无向完整图中为每个边缘分配方向而获得的有向图(有向图)。 也就是说,它是一个完整图形的方向,等价于一个有向图,其中每对不同的顶点通过单个有向边连接,即每对顶点之间都有一条边相连的有向图称为竞赛图。1
兰多(1953)首先调查了竞赛图的许多重要属性。竞赛图的当前应用包括投票理论和社会选择理论的研究等。 竞赛图起源于这样的图形解释:循环赛,其中每个玩家恰好一次遇到每个其他玩家。 在竞赛图中,顶点对应于球员。 每对玩家之间的边缘从胜者到失败者。 如果每个玩家都对阵同样数量的其他玩家,那么这个竞赛图就被称之为常规竞赛图。2
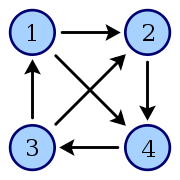
路径和循环任何有限数量n个顶点的竞赛图都包含一个哈密尔顿路径,即所有n个顶点上的直线路径。假设该语句适用于n,并考虑n + 1个顶点上的任何竞赛图T。 选择T的顶点v0,并考虑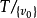 的一个有向路径
的一个有向路径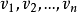 。现在让
。现在让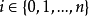 是最大的,所以对于每个
是最大的,所以对于每个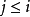 都有一个从
都有一个从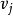 到
到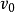 的有向边。
的有向边。
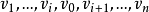
是根据需要设置的有向路径。 这个参数还给出了一种求解哈密尔顿算子的算法。 只需要检查边缘的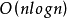 。
。
这意味着紧密联系的竞赛图有一个哈密尔顿循环(Camion 1959)。 每个联系的竞赛图是顶点泛循环:对于每个顶点v,并且每个k在竞赛图中的三个到顶点的数量的范围内,存在包含v的长度为k的循环。此外,如果比赛是4连接的,则每对顶点可以与哈密尔顿路径连接(Thomassen 1980)。
传递性在竞赛图中,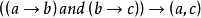 被叫做一个传递。换句话说,在传递竞赛图中,顶点(严格地)由边缘关系完全排序。
被叫做一个传递。换句话说,在传递竞赛图中,顶点(严格地)由边缘关系完全排序。
等价条件以下语句与n个顶点上的竞赛图T相当:
(1)T具有传递性;
(2)T是一个严格的总排序;
(3)T是非循环的;
(4)T不包含长度为3的循环;
(5)T的得分序列(外差集)为{0,1,2,...,n-1};
(6)T只有一个哈密尔顿路径。
拉姆齐理论传递竞赛图在拉姆齐理论中起到类似于无向图中的作用。 特别是,n个顶点上的每个竞赛图在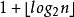 顶点上包含一个传递子公式。证明很简单:选择任何一个顶点v作为这个子公式的一部分,并在v的输入邻集或v的传出邻集之间递归地形成其余的子体,然后取较大者。
顶点上包含一个传递子公式。证明很简单:选择任何一个顶点v作为这个子公式的一部分,并在v的输入邻集或v的传出邻集之间递归地形成其余的子体,然后取较大者。
缩合任何比赛的本身就是一场传递性的比赛。 因此,即使是不可传递的比赛,竞赛图的强力连接组件也可能被完全排序。
得分序列和分数集比赛的得分序列是比赛顶点的不规则序列。 比赛的得分集是在该比赛中顶点的偏差的整数集合。
Landau的定理(1953):整数序列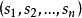 当且仅当满足下面条件的时候是一个得分序列:
当且仅当满足下面条件的时候是一个得分序列:
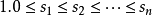
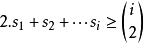
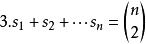
让s(n)是大小为n的不同得分序列的数量。 序列s(n)(OEIS中的序列A000571)开始为:
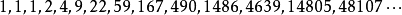
温斯顿和克莱特曼证明,对于足够大的n:
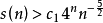
其中c1= 0.049。
这些提供证据表明:
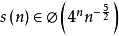
这里φ表示一个渐近紧的界限。
姚明表示,每一个非空的整数都是一些比赛的得分。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国