定义
含有3个未知数,并且含有未知数的项的次数都是1的整式方程叫做三元一次方程,可化为一般形式ax+by+cz=d(a、b、c≠0)或ax+by+cz+d=0(a、b、c≠0)。
三元一次方程的解适合一个三元一次方程的每一对未知数的值,叫做这个三元一次方程的一个解。对于任何一个三元一次方程,令其中两个未知数取任意两个值,都能求出与它对应的另一个未知数的值。因此,任何一个三元一次方程都有无数多个解,由这些解组成的集合,叫做这个三元一次方程的解集。
例如,三元一次方程: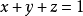 ,解有无数个
,解有无数个
当 时,
时,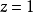
当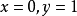 时,
时,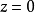
...
当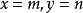 时,
时,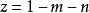
与空间平面数学课程 中的方程与空间几何图形比如平面、曲面、直线、曲线是有对应关系的,三元一次方程就与空间几何图形——空间平面相对应。 一些特殊的三元一次方程,比如常数项为零、或者只含有两个未知数 、或者只含有一个未知数的就会与一些特殊的空间平面相对应。1
已知平面上的一点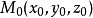 和它的一个法线向量
和它的一个法线向量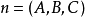 , 对平面上的任一 点
, 对平面上的任一 点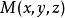 ,有向量
,有向量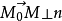 ,
,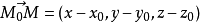 。由空间两个向量垂直的充要条件有,
。由空间两个向量垂直的充要条件有,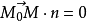 ,代入坐标有:
,代入坐标有:
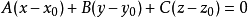
上式为空间平面的点法式方程。注意到该方程是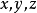 的一次方程,故可推定 :任一平面都可以用三元一次方程来表示。这是因为任一平面都可以由它的法向量与它上面的一点唯一决定,而平面的点法式方程本身就是三元一次方程。
的一次方程,故可推定 :任一平面都可以用三元一次方程来表示。这是因为任一平面都可以由它的法向量与它上面的一点唯一决定,而平面的点法式方程本身就是三元一次方程。
反过来,若有三元一次方程
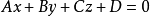
任取满足该方程的一组数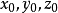 ,即
,即

两式相减,得: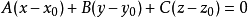 ,该方程是过点
,该方程是过点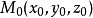 且以
且以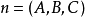 为法向量的平面方程。由此可知,三元一次方程所代表的图形是平面。
为法向量的平面方程。由此可知,三元一次方程所代表的图形是平面。
三元一次方程组定义由多个一元一次方程组成并含有三个未知数的方程组叫做三元一次方程组
例如: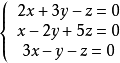
注意:每个方程不一定都含有三个未知数,但方程组整体上要含有三个未知数。
求解思路解三元一次方程组的基本思想仍是消元,其基本方法是代入消元法和加减消元法。
步骤:
①利用代入法或加减法,消去一个未知数,得到一个二元一次方程组;
②解这个二元一次方程组,求得两个未知数的值;
③将这两个未知数的值代入原方程中含有三个未知数的一个方程,求出第三个未知数的值,把这三个未知数的值用一个大括号写在一起就是所求的三元一次方程组的解。2
举例例1
解三元一次方程组
解:
对方程组中得方程进行标号
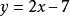 ①
①
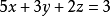 ②
②
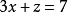 ③
③
对方程组进行分析:该方程组可用代入法先消去y,把①代入②,得,
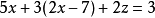 即
即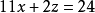
解二元一次方程组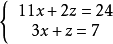 ,得:
,得: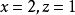
把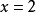 代入①中,得
代入①中,得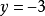
所以,这个方程组的解为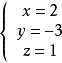
例2
解三元一次方程组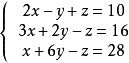
解:
对方程组进行标号,
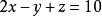 ①
①
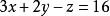 ②
②
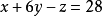 ③
③
对方程组进行分析:从三个方程的未知数的系数特点来考虑,先消z比较简单。
①+②得,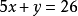 ④
④
①+③得,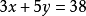 ⑤
⑤
④与⑤组成一个二元一次方程组,解这个方程组,得 x、y值;把x、y值方程③,得z值。
注意:为把三元一次方程组转化为二元一次方程组,原方程组中的每个方程至少要用一次。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国