[科普中国]-真值表

离散数学定义

真值表是含n(n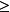1)命题变项的命题公式 ，共有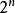组赋值将命题公式A在所有赋值之下取值的情况列成表，称为A的真值表。1

构造真值表步骤

找出命题公式中所含的所有命题变项（若无下角标就按字典顺序给出），列出所有的可能的赋值（）；

按从低到高的顺序写出各层次；

对应每个赋值，计算命题公式各层次的值，直到最后计算出命题公式的值。

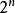
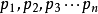
真值表的发展发明真值表是用来在弗雷格、罗素等人开发的命题演算上工作的。它是在1917年年由维特根斯坦首次和1921年由 Emil Post 独立发明的。真值表最初是作为一项逻辑矩阵的发现而产生的，十九世纪卓越的逻辑学家，美国人查尔士·山德尔斯·皮尔士以这项逻辑矩阵的发现为命题逻辑现代系统做出了重大贡献。维特根斯坦的逻辑哲学论使用它们把真值函数置于序列中。这个著作的广泛影响导致了真值表的传播。

真值表被用来计算真值泛函表达式的值(就是说是一个判定过程)。真值泛函表达式要么是原子(就是说是命题变量(或占位符)或命题函数 - 比如 Px)或建造自使用逻辑运算符(就是说 ∧ (AND)，∨ (OR)，¬ (NOT) - 例如 Fx & Gx)的原子公式。

真值表中的列标题展示了 (i) 命题函数与/或变量，和 (ii) 建造自这些命题函数或变量和运算符的真值泛函表达式。行展示对 (i) 和 (ii) 的 T 或 F 指派的每个可能的求值。换句话说，每行都是对 (i) 和 (ii) 的不同解释。

实例经典(就是说二值)逻辑的真值表限定于只有两个真值是可能的布尔逻辑系统，它们是真或假，通常在表中简单的表示为 T 和 F。

举例：用真值表方法回答：丁的话是否成立？为什么？

甲：只有小王不上场，小李才上场。

乙：如果小王上场，则小李上场。

丙：小王上场，当且仅当小李不上场。

丁：甲、乙、丙的话都不对。

解答：列表：

p q —pq p—q

真 真 假 真 假

真 假 真 假 真

假 真 真 真 真

假 假 真 真 假

由表可知，丁的话不能成立，因为甲、乙、丙三人的话不可能同时为假。

分析：以往的真值表解题，大都是要求判定两个判断是否等值或是否矛盾。近来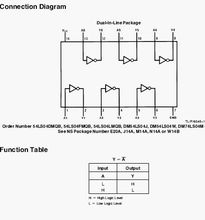，一些真值表解题的要求有所改变，增加了试题考核的能力与难度层次。本例题就是一种类型。题目要求判定“丁的话是否成立”，实质上是要判定甲、乙、丙的话能否同假。

此类题目往往以自然语句出现，又规定了要用真值表方法解题，所以答题时的要领有以下几个：一是把自然语句正确形式化，二是准确列出真值表，尤其是要小心求出判断的真值，三是根据真值表作出判断。

实例 2： 如果他是理科学生，他必学好数学。如果他不是文科
学生，他必是理科学生。他没有学好数学。所以他是文科学生。
试用真值表法判断此推理是否有效？2解：设 P：他是理科学生，Q：他学好数学，R：他是文科学
生，则该命题推理的前提是：P → Q，┐ R → P，┐ Q；结论是：
R。于是，此题可以表述为：（P → Q）∧（┐ R → P）∧┐ Q R。
下面用真值表法来判断此命题是否有效。（设 E=（P → Q）∧
（┐ R → P）∧┐ Q）由上表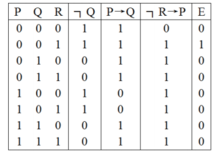知，当命题（P → Q）∧（┐ R → P）∧┐ Q 的真
值为 1 时，R 的真值也是 1，所以，（P → Q）∧（┐ R → P）
∧┐ Q → R 是重言式，故该推理是有效的。