[科普中国]-几何学

名称来源

几何这个词最早来自于阿拉伯语，指土地的测量，即测地术。后来拉丁语音译为“geometria”。中文中的“几何”一词，最早是在明代利玛窦、徐光启合译《几何原本》时，由徐光启所创。当时并未给出所依根据，后世多认为一方面几何可能是拉丁化的希腊语GEO的音译，另一方面由于《几何原本》中也有利用几何方式来阐述数论的内容，也可能是magnitude（多少）的意译，所以一般认为几何是geometria的音、意并译。

1607年出版的《几何原本》中关于几何的译法在当时并未通行，同时代也存在着另一种译名——形学，如狄考文、邹立文、刘永锡编译的《形学备旨》，在当时也有一定的影响。在1857年李善兰、伟烈亚力续译的《几何原本》后9卷出版后，几何之名虽然得到了一定的重视，但是直到20世纪初的时候才有了较明显的取代形学一词的趋势，如1910年《形学备旨》第11次印刷成都翻刊本徐树勋就将其改名为《续几何》。直至20世纪中期，已鲜有“形学”一词的使用出现。

诞生由于人类生产和生活的需要，产生了几何学。

在原始社会里，人类在生产和生活中，积累了许多有关物体的形状、大小和相互之间的位置关系的知识。例如，古代的人们认识他们的猎物的形状、大小，记住它们的居住地与打猎地之间的距离，以及打猎地在居住地的那个方位。

随着人类社会的不断发展，人们对物体的形状、大小和相互之间的位置关系的认识愈来愈丰富，逐渐地积累起较丰富的几何学知识。

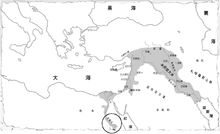相传四千年前，埃及的尼罗河每年洪水泛滥，总是把两岸的土地淹没，水退后，使土地的界线不分明。当时埃及的劳动人民为了重新测出被洪水淹没的土地的地界，每年总要进行土地测量，因此，积累了许多测量土地方面的知识。从而产生了几何学的初步知识。

后来，希腊人由于跟埃及人通商，从埃及学到了测量与绘画等的几何初步知识。希腊人在这些几何初步知识的基础上，逐步充实并提高成为一门完整的几何学。“几何学”这个词，是来自希腊文，原来的意义是“测量土地技术”。“几何学”这个词一直沿用到今天。

公元前338年，希腊人欧几里得，把在他以前的埃及和希腊人的几何学知识加以系统的总结和整理，写了一本书，书名叫做《几何原本》。1607年，我国的数学家徐光启和西方人利玛窦合作，把欧几里得的《几何原本》第一次介绍到我国。欧几里得的《几何原本》是几何学史上有深远影响的一本书。现今我们学习的几何学课本多是以《几何原本》为依据编写的。

我国对几何学的研究也有悠久的历史。在公元前一千年前，在我国的黑陶文化时期，陶器上的花纹就有菱形、正方形和圆内接正方形等许多几何图形。公元前五百年，在墨翟所著的《墨经》里有几何图形的一些知识。在《九章算术》里，记载了土地面积和物体体积的计算方法。在《周髀算经》里，记载了直角三角形的三边之间的关系。这就是著名的“勾三股四弦五”的勾股定理，也称为“商高定理”。商高发现了直角三角形的勾股定理。祖冲之的圆周率也是著称世界的。还有我国古代数学家刘徽、王孝通等对几何学都作出了重大的贡献。

随着工农业生产和科学技术的不断发展，几何学的知识也越来越丰富，研究的方面也越来越广阔。

发展历史几何一词源于《几何原本》的翻译。《几何原本》是世界数学史上影响最为久远，最大的一部数学教课书。《几何原本》传入中国，首先应归功于明末科学家徐光启。徐光启和利玛窦《几何原本》中译本的一个伟大贡献是确定了研究图形的这一学科中文名称为“几何”，并确定了几何学中一些基本术语的译名。“几何”的原文是“geometria”(英文geometry)，徐光启和利玛窦在翻译时，取“geo”的音为“几何”（明朝音: gi-ho），而“几何”二字中文原意又有“衡量大小”的意思。用“几何”译“geometria”(英文geometry)，音义兼顾，确是神来之笔。几何学中最基本的一些术语，如点、线、直线、平行线、角、三角形和四边形等中文译名，都是这个译本定下来的。这些译名一直流传到今天，且东渡到汉字文化圈的日本、朝鲜等国（越南语则使用独自翻译的越制汉语“形学（hình học）”一词），影响深远。

几何学开始的最早记录可以追踪到公元前2世纪的古代埃及和美索不达米亚。早期的几何学是有关长度、角度、面积和体积的经验性定律的收集，这些都是因为实际需要（比如勘探、建筑、天文和一些手工业）而发展的。最早的已知有关几何学的文本是埃及的莱因德纸草书（公元前2000-1800年）和莫斯科纸草书（英语：Moscow Mathematical Papyrus）（约公元前1890年）,以及古巴比伦的泥石板（比如“Plimpton 322（英语：Plimpton 322）”（公元前1900年）。比如，莫斯科纸草书上给出了如何计算棱台体积的公式。埃及南部的古代努比亚人曾经建立了一套几何学系统，包括有太阳钟的早期版本。

几何学有悠久的历史。最古老的欧氏几何基于一组公设和定义，人们在公设的基础上运用基本的逻辑推理构做出一系列的命题。可以说，《几何原本》是公理化系统的第一个范例，对西方数学思想的发展影响深远。

一千年后，笛卡儿在《方法论》的附录《几何》中，将坐标引入几何，带来革命性进步。从此几何问题能以代数的形式来表达。

欧几里得几何学的第五公设，由于并不自明，引起了历代数学家的关注。最终，由罗巴切夫斯基和黎曼建立起两种非欧几何。

几何学的现代化则归功于克莱因、希尔伯特等人。克莱因在普吕克的影响下，应用群论的观点将几何变换视为特定不变量约束下的变换群。而希尔比特为几何奠定了真正的科学的公理化基础。应该指出几何学的公理化，影响是极其深远的，它对整个数学的严密化具有极其重要的先导作用。它对数理逻辑学家的启发也是相当深刻的。

古代几何几何最早的有记录的开端可以追溯到古埃及（参看古埃及数学），古印度（参看古印度数学），和古巴比伦（参看古巴比伦数学），其年代大约始于公元前3000年。早期的几何学是关于长度，角度，面积和体积的经验原理，被用于满足在测绘，建筑，天文，和各种工艺制作中的实际需要。在它们中间，有令人惊讶的复杂的原理，以至于现代的数学家很难不用微积分来推导它们。例如，埃及和巴比伦人都在毕达哥拉斯之前1500年就知道了毕达哥拉斯定理（勾股定理）；埃及人有方形棱锥的锥台（截头金字塔形）的体积的正确公式；而巴比伦有一个三角函数表。

中国文明和其对应时期的文明发达程度相当，因此它可能也有同样发达的数学，但是没有那个时代的遗迹可以使我们确认这一点。也许这是部分由于中国早期对于原始的纸的使用，而不是用陶土或者石刻来记录他们的成就。

古代成就古埃及人的几何学成就，主要有以下两点

1．每年的雨季，尼罗河水泛滥，淹没了两岸的耕地。雨季过后河水退去，留下肥沃的土地，古埃及就开始耕种。为了恢复各人田产的界线，就需要重新丈量，这就使得古埃及人的几何学逐渐发达起来。

2．古埃及人为死去的法老建造的陵墓金字塔，是由一块块巨石砌成的。在长年累月的建造活动中，埃及人的立体几何学也发展起来，他们能够把很多块巨石精确切割之后运到工地，再砌成雄伟的金字塔。石块之间对接紧密，而且整座金字塔浑然一体，表现出高超的技术水平。

分支学科平面几何

立体几何

非欧几何

罗氏几何

黎曼几何

解析几何

射影几何

仿射几何

代数几何

微分几何

计算几何

拓扑学

欧几里德公元前3世纪中叶，埃及国王托勒密一世问一位数学家：有没有不学习《几何原本》，即可掌握几何学的捷径。数学家断言回答：世界上没有通向几何的平易之路。这位数学专家就是《几何原本》的作者、古希腊大名鼎鼎的欧几里德。

学园生活欧几里得（Euclid）是古希腊著名数学家、欧氏几何学的开创者。欧几里得生于雅典，当时雅典就是古希腊文明的中心。浓郁的文化气氛深深地感染了欧几里得，当他还是个十几岁的少年时，就迫不及待地想进入“柏拉图学园”学习。

一天，一群年轻人来到位于雅典城郊外林荫中的“柏拉图学园”。只见学园的大门紧闭着，门口挂着一块木牌，上面写着：“不懂数学者，不得入内！ ”这是当年柏拉图亲自立下的规矩，为的是让学生们知道他对数学的重视，然而却把前来求教的年轻人给闹糊涂了。有人在想，正是因为我不懂数学，才要来这儿求教的呀，如果懂了，还来这儿做什么?正在人们面面相觑，不知是退、是进的时候，欧几里得从人群中走了出来，只见他整了整衣冠，看了看那块牌子，然后果断地推开了学园大门，头也没有回地走了进去。

“柏拉图学园”是柏拉图40岁时创办的一所以讲授数学为主要内容的学校。在学园里，师生之间的教学完全通过对话的形式进行，因此要求学生具有高度的抽象思维能力。数学，尤其是几何学，所涉及的对象就是与真、普遍而抽象的东西。它们同生活中的事物有关，但是又不来自于这些具体的事物，因此学习几何被认为是寻求真理的最有效的途径。柏拉图甚至声称：“上帝就是几何学家。”这一观点不仅成为学园的主导思想，而且也为越来越多的希腊民众所接受。人们都逐渐地喜欢上了数学，欧几里得也不例外。他在有攀滋入学园之后，便全身心地沉潜在数学王国里。他潜心求索，以继器柏拉图的学术为奋斗目标，除此之外，他哪儿也不去，什么也不干。熬翻阅和研究了柏拉图的所有著作和手稿，可以说，连柏拉图的亲传攀擎也没有谁能像他那样熟悉柏拉图的学术思想、数学理论。经过对柏拉图思想的深入探究，他得出结论：图形是神绘制的，所有一切抽象的逻辑规律都体现在图形之中。因此，对智慧的训练，就应该以图形为主要研究对象的几何学开始。他确实领悟到了柏拉图思想的要旨，并开始沿着柏拉图当年走过的道路，把几何学的研究作为自学主要任务，并最终取得了世人敬仰的成就。

名称来源最早的几何学兴起于公元前7世纪的古埃及，后经古希腊数学家泰勒斯等人传到古希腊的米利都城，又借毕达哥拉斯学派经典。在欧几里德以前，人们已经积累了许多几何学的知识，然而这些知识当中，存在一个很大的缺点和不足，就是缺乏系统性。大多数是片断、零碎的知识，公理与公理之问、证明与证明之间并没有什么很强的联系性，更不要说对公式和定理进行严格的逻辑论证和说明。因此，随着社会经济的繁荣和发展，特别是随着农林畜牧业的发展、土地开发和利用的增多，把这些几何学知识加以条理化和系统化，成为一整套可以自圆其说、前后贯通的知识体系，已经是刻不容缓，成为科学进步的大势所趋。欧几里德通过早期对柏拉图数学思想，尤其是几何学理论系统而周详的研究，已敏锐地察觉到了几何学理论的发展趋势。他下定决心，要在有生之年完成这一工作。为了完成这一重任，欧几里德不辞辛苦，长途跋涉，从爱琴海边的雅典古城，来到尼罗河流域的埃及新埠——亚历山大城，为的就是在这座新兴的，但文化蕴藏丰富的异域城市实现自己的初衷。在此地的无数个日日夜夜里，他一边收集以往的数学专著和手稿，向有关学者请教，一边试着著书立说，阐明自己对几何学的理解，哪怕是尚肤浅的理解。经过欧几里德忘我的劳动，终于在公元前300年结出丰硕的果实，这就是几经易稿而最终定形的《几何原本》一书。这是一部传世之作，几何学正是有了它，不仅第一次实现了系统化、条理化，而且又孕育出一个全新的研究领域——欧几里德几何学，简称“欧氏几何学”1。

平面几何《几何原本》是一部集前人思想和欧几里德个人创造性于一体的不朽之作。传到今天的欧几里德著作并不多，然而我们却可以从这部书详细的写作笔调中，看出他真实的思想底蕴。

全书共分13卷。书中包含了5条“公理”、5条“公设”、23个定义和467个命题。在每一卷内容当中，欧几里德都采用了与前人完全不同的叙述方式，即先提出公理、公设和定义，然后再由简到繁地证明它们。这使得全书的论述更加紧凑和明快。而在整部书的内容安排上，也同样贯彻了他的这种独具匠心的安排。它由浅到深，从简至繁，先后论述了直边形、圆、比例论、相似形、数、立体几何以及穷竭法等内容。其中有关穷竭法的讨论，成为近代微积分思想的来源。仅仅从这些卷帙的内容安排上，我们就不难发现，这部书已经基本囊括了几何学从公元前7世纪的古埃及，一直到公元前4世纪——欧几里德生活时期——前后总共400多年的数学发展历史。这其中，颇有代表性的便是在第1卷到第4卷中，欧几里德对直边形和圆的论述。正是在这几卷中，他总结和发挥了前人的思维成果，巧妙地论证了毕达哥拉斯定理，也称“勾股定理”。即在一直角三角形中，斜边上的正方形的面积等于两条直角边上的两个正方形的面积之和。他的这一证明，从此确定了勾股定理的正确性并延续了2000多年。《几何原本》是一部在科学史上千古流芳的巨著。它不仅保存了许多古希腊早期的几何学理论，而且通过欧几里德开创性的系统整理和完整阐述，使这些远古的数学思想发扬光大。它开创了古典数论的研究，在一系列公理、定义、公设的基础上，创立了欧几里德几何学体系，成为用公理化方法建立起来的数学演绎体系的最早典范。照欧氏几何学的体系，所有的定理都是从一些确定的、不需证明而且为真的基本命题即公理演绎出来的。在这种演绎推理中，对定理的每个证明必须或者以公理为前提，或者以先前就已被证明了的枣理为前提，最后做出结论。这一方法后来成了用以建立任何知识体系的严格方式，人们不仅把它应用于数学中，也把它应用于科学，丽且也应用于神学甚至哲学和伦理学中，对后世产生了深远的影响。尽管欧几里德的几何学在差不多2000年间，被奉为严格思维的几乎无懈可击的范例，但实际上它并非总是正确的。人们发现，一些欧几里德作为不证自明的公理，却难以自明，越来越遭到怀疑。比型“第五平行公理”，欧几里德在《几何原本》一书中断言：“通过已知外一已知点，能作且仅能作一条直线与已知直线平行。”这个结果在普通平面当中尚能够得到经验的印证，那么在无处不在的闭合球面之中（地球就是个大曲面）这个平行公理却是不成立的。黔俄国人罗伯切夫斯基和德国人黎曼由此创立了球面几何学，即取几里得几何学。

求知路欧几里德不仅是一位学识渊博的数学家，同时还是一位有“温和仁慈的蔼然长者 ”之称的教育家。在著书育人过程中，他始终没有忘记当年挂在“柏拉图学园”门口的那块警示牌，牢记着柏拉图学派自古承袭的严谨、求实的传统学风。他对待学生既和蔼又严格，自己却从来不宣扬有什么贡献。对于那些有志于穷尽数学奥秘的学生，他总是循循善诱地予以启发和教育，而对于那些急功近利、在学习上不肯刻苦钻研的人，则毫不客气地予以批评。在柏拉图学派晚期导师普罗克洛斯的《几何学发展概要》中，就记载着这样一则故事，说的是数学在欧几里德的推动下，逐渐成为人们生活中的一个时髦话题（这与当今社会截然相反），以至于当时托勒密国王也想赶这一时髦，学点儿几何学。虽然这位国王见多识广，但欧氏几何却在他的智力范围之外。于是，他问欧几里德，学习几何学有没有什么捷径可走岁欧几里德严肃地说：“抱歉，陛下!学习数学和学习一切科学一样，是没有什么捷径可走的。学习数学，人人都得独立思考，就像种庄稼一样，不耕耘是不会有收获的”。在这一方面，国王和普通老百姓是一样的。”

欧几里德是人类科学思想史上的一盏指路明灯。他第一次使数学理论系统化，并使几何学逐渐成为一门独立发展的正式学科体系。他对数学史上的许多疑难命题和定理做了开创性的论证和解释，为数学的发展打下了坚实的理论基础，而他在理论中存在的映撼，也成为后人攀越智慧高峰不可缺少的台阶。这一正一反都推动了人类数学思想的进步，从而为后来人类能更好、更深刻的认识自然界提供了更为有效的工具。因此，后人尊称他为“几何学之父”，以铭记他在数堂胃相中卜的卓越贡献。

我们已无法考察欧几里德的生世，只知道他给这个世界上留了一本书与两句话，其中一句话是面对一位青年关于几何学的问题，这个青年问：你的几何学有何用处。他的回答是：“请给这个小伙子3个硬币，因为他想从几何学里得到实际利益。”由此可知，欧几里德也是一位伟大的哲学家！

欧式现代杨振宁曾发表演说，认为现代科学没有发生在中国而是发生在西方，正是因为《几何原本》和《周易》所产生的影响。这种影响直接导致了两种思维方式、两种文化。杨振宁的讲演曾经引起力挺《周易》学者的强烈不满。然而同样是中华文化的支持者聂文涛却认为，欧几里德所导致的直观思维导致西方学者热衷于解剖研究和物体运动轨迹研究，因此会有两部影响世界的图书问世，这就是《心血运动论》和《天体运行论》。然而，东方思维下将会更有利于对生命的尊重和理解，因此一旦与现代科技相融合则必然会引发生命科学领域的巨大发展。

总之，欧几里德所产生的影响超越了时间和空间，并将在可以预见的未来中不断发生影响。

相关名言几何学的简洁美却又正是几何学之所以完美的核心存在。——牛顿

几何看来有时候要领先於分析，但事实上，几何的先行於分析，只不过像一个仆人走在主人的前面一样，是为主人开路的。——西尔维斯特

分形几何不仅展示了数学之美，也揭示了世界的本质，还改变了人们理解自然奥秘的方式；可以说分形几何是真正描述大自然的几何学，对它的研究也极大地拓展了人类的认知疆域。——周海中

笛卡儿的解析几何于牛顿的微积分已被扩张到罗巴切夫斯基、黎曼、高斯和塞尔维斯托的奇异的数学方法中。事实上，数学不仅是各门学科所必不可少的工具，而且它从不顾及直观感觉的约束而自由地飞翔着。——尼古拉斯·默里·巴特勒