[科普中国]-完全图

简介

在图论的数学领域，完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。完整的有向图又是一个有向图，其中每对不同的顶点通过一对唯一的边缘（每个方向一个）连接。n个端点的完全图有n个端点以及n(n − 1) / 2条边，以Kn表示。它是(k − 1)-正则图。所有完全图都是它本身的团（clique）。

图形理论本身以莱昂哈德欧拉于1736年在Königsberg七桥的工作开始。 然而，完全图的绘图，其顶点放置在正多边形的点上，已经在13世纪中出现。这样的绘画有时被称为神秘玫瑰。1

属性n个顶点的完全图表示为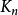 。 一些消息来源称，这个符号中的字母K代表德语单词komplett，但完全图的德文名称vollständigerGraph不包含字母K，其他来源则表示符号表示 Kazimierz Kuratowski图论。

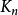具有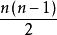 个边（三角数），并且是维度为n-1的常规图。所有完全图都是它们自己的最大组。 它们是最大化连接的，因为断开图形的唯一顶点是所有的顶点集。完全图的补码图是一个空图。

如果一个完全图的边缘都被赋予一个方向，那么所得的有向图就被称为比赛。

完全图的匹配数由电话号码给出：

1，1，2，4，10，26，76，232，764，2620，9496，35696，140152，568504，2390480，10349536，46206736，...（OEIS中的序列A000085）。

这些数字给出了n顶点图的Hosoya索引的最大可能值。完全图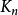 （n均匀）完美匹配的数量由双因子 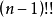给出。

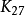的交叉号码是已知的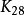， 需要7233或7234个交叉口。 进一步的值是由直线交叉号码项目收集的。 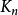的交叉数字是：

0,0,0,0,1,3,9,29,36,62,102,153,229,324,447,603,798,1029,1318,1657,2055,2528,3077,3699,4430,5250,6180，...（OEIS中的序列A014540）。

几何和拓扑具有n个节点的完全图表示（n-1） - 复杂的边缘。 几何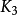 形成三角形的边缘集合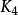， 是四面体等。具有圆环拓扑的非凸多面体Császár多面体具有完整的图形 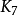作为其骨架。 四个或更多维度的每个多面体也具有完整的框架。

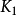至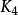 均为平面图。 然而，具有五个或更多个顶点的完整图形的每个平面图都必须包含交叉点，并且非平面完全图 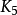在平面图的表征中起关键作用：通过库拉托斯基定理，当且仅当它既不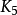包含 也不是包含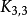 作为细分，图才能成为平面图，通过瓦格纳定理，图形代替细分也是一样的结果。 康威和戈登证明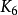， 在三维空间中的每一次嵌入是内在联系的，至少有一对连接的是三角形。 康威和戈登还表明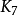， 的任何三维嵌入包含一个嵌入在空间中的哈密尔顿循环。

举例n顶点的完全图，在n从1到12之间，与边缘数量一起显示如下：

无向完全图无向完全图是用n表示图中顶点数目的一种图，一张图中每条边都是无方向的。2

定义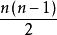 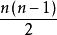用n表示图中顶点数目，用e表示边或弧的数目。若∈VR，则vi≠vj，那么，对于无向图，e的取值范围是0到，有条边的无向图称为完全图。

解释直观来说，若一个图中每条边都是无方向的，则称为无向图。

（1）无向边的表示

无向图中的边均是顶点的无序对，无序对通常用圆括号表示。

【例】无序对(vi，vj)和(vj，vi)表示同一条边。

（2）无向图的表示

【例】下面(b)图中的G2和(c)图中的G3均是无向图，它们的顶点集和边集分别为：

V(G2)={v1，v2，v3，v4}

E(G2)={(vl，v2)，(v1，v3)，(v1，v4)，(v2，v3)，(v2，v4)，(v3，v4)}

V(G3)={v1，v2，v3，v4，v5，v6，v7}

E(G3)={(v1，v2)，(vl，v3)，(v2，v4)，(v2，v5)，(v3，v6)，(v3，v7)}

注意在以下讨论中，不考虑顶点到其自身的边。即若(v1，v2)或是E(G)中的一条边，则要求v1≠v2。此外，不允许一条边在图中重复出现，即只讨论简单的图。

3．图G的顶点数n和边数e的关系

（1）若G是无向图，则0≤e≤n(n-1)/2

恰有n(n-1)/2条边的无向图称无向完全图(Undirected Complete Graph)

（2）若G是有向图，则0≤e≤n(n-1)。

恰有n(n-1)条边的有向图称为有向完全图(Directed Complete Graph)。

注意：

完全图具有最多的边数。任意一对顶点间均有边相连。

【例】上面(b)图的G2就是具有4个顶点的无向完全图。

有向完全图用n表示图中顶点数目，用e表示边或弧的数目。若∈VR，则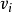≠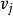，那么，对于有向图，e的取值范围是0到 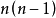，有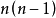 条边的有向图称为有向完全图。3