简述
正四面体正四面体是五种正多面体中的一种,有4个正三角形的面,4个顶点,6条棱。正四面体不同于其它四种正多面体,它没有对称中心。正四面体有六个对称面,其中每一个都通过其一条棱和与这条棱相对的棱的中点。正四面体很容易由正方体得到,只要从正方体一个顶点A引三个面的对角线AB,AC,AD,并两点两点连结之即可。正四面体和一般四面体一样,根据保利克-施瓦兹定理能够用空间四边形及其对角线表示。正四面体的对偶是其自身。1
定义正四面是由四个全等的正三角形所组成的几何体。它有四个面、四个顶点、六条棱。每个二面角均为70°32’,有四个三面角,每个三面角的面角均为60°,以a表示棱长,A表示全面积,V表示体积,则
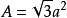
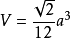 2
2
性质1.正四面体的每一个面是正三角形,反之亦然。
2.正四面体是三组对棱都垂直的等面四面体。
3.正四面体是两组对棱垂直的等面四面体。
4.正四面体的对棱中点的连线都互相垂直且相等,等于棱长的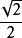 倍,反之亦真。
倍,反之亦真。
5.正四面体的各棱的中点是正八面体的六顶点。
6.正四面体的全面积是棱长平方的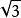 倍,体积是棱长立方的
倍,体积是棱长立方的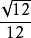 倍。
倍。
7.正四面体的四个旁切球半径均相等,等于内切球半径的2倍,或等于四面体高线的一半。
8.正四面体的内切球与各侧而的切点是侧I面三角形的外心,或内心,或垂心,或重心,除外心外,其逆命题均成立。
9.正四面体的外接球球心到四面体四顶点的距离之和,小于空间中其他任一点到四顶点的距离之和。
10.正四面体内任意一点到各侧面的垂线长的和等于这四面体的高。
11.对于四个相异的平行平面,总存住一个正四面体,其顶点分别在这四个平面上。
12.以正四面体的每条棱为直径作球,设S是所作六个球的交集,则S中含有两点,它们的距离为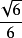 倍棱长。
倍棱长。
13.过正四面体的一棱及所对的棱的中点的截面面积与其侧面三角形面积之比为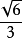 。
。
14.四面体为正四面体的充要条件是,其棱均做为外接平行六面体的侧面对角线时,平行六面体为正方体。
15.四面体为正四面体的充要条件是,其共顶点三i棱作为外接平行六面体的棱时,平行六面体为一个三面角面角均为60°的菱形六面体。
16.四面体为正四体的充要条件是,四面体在平行于两棱的每一个平面的射影是正方形。
17.四面体为正四面体的充要条件是,四面体的展开图是一个引出了三条中位线的正三角形。
18.正四面体每条高的中点与底面三角形三顶点均构成直角四面体的四顶点,且高的中点为址三面角顶点。3
相关计算当正四面体的棱长为a时,一些数据如下:
高: 。中心把高分为1:3两部分。
。中心把高分为1:3两部分。
表面积: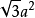
体积: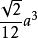
对棱中点的连线段的长: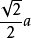
外接球半径: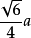
内切球半径: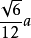
两条高夹角: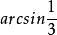
侧棱与底面的夹角: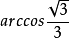




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国