[科普中国]-第一象限

简介

象限，又称象限角（英文：Quadrant意思是一圆之四分一等份），是直角坐标系（笛卡尔坐标系）中，主要应用于三角学和复数的阿根图（复平面）中的坐标系。平面直角坐标系里的横轴和纵轴所划分的四个区域，分为四个象限。象限以原点为中心，x，y轴为分界线。右上的称为第一象限，左上的称为第二象限，左下的称为第三象限，右下的称为第四象限。坐标轴上的点不属于任何象限。

特点第一象限中的点的横坐标大于0，纵坐标也大于0。

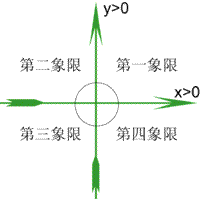在数轴上0点处再加一条垂直直线,就成了一个笛卡儿坐标图,右上角那一块区域称为第一象限,上面左边那一块为第二象限,第二象限的下面为第三象限,然后第一象限的下面,即第三象限的右边称做第四象限。这时角的概念就是x轴正方向那条射线(右边那条),绕O点逆时针转过的角度.可以绕很多圈,比如绕了2圈又回到x轴正方向,那这个角就为720度。

第一象限：（正+,+正），横纵坐标同号，记作xy>0。

角的度数只要这条射线最终落在第一象限,(不包括x,y轴),就称为第一象限角,有我们通常熟悉的0-90度,还有360-450 ,720-810等。

在第一象限的角的sin值，cos值，tan值均为正数。

可以看该角的终边上的任意一点的坐标（x,y）

x>0,y>0时在第一象限

x0时在第二象限

x