[科普中国]-纽结理论

简介

纽结理论是数学学科代数拓扑的一个分支，按照数学上的术语来说，是研究如何把若干个圆环嵌入到三维实欧氏空间中去的数学分支。纽结理论的特别之处是它研究的对象必须是三维空间中的曲线。在两维空间中，由于没有足够的维数，我们不可能把让一根曲线自己和自己缠绕在一起打成结；而在四维或以上的空间中，由于维数太多，无论怎么样的纽结都能够很方便地被解开成没有结的曲线。

基本问题绳结是人人熟悉的，史前时期就有结绳记事。试一试就会相信，图1中的两个结不一样：没法把一个变形成另一个，除非把绳头抽回重穿。绳子的粗细、长短、曲直允许改变，单单不许绳头重穿。由于这条规矩不易精确描述，那么索性规定绳的两端要捻合起来（于是刚才的两个结要改画成图2）。这样就可以得到了数学上的定义：纽结是三维空间中的不与自己相交的封闭曲线，或者

说，三维空间中的与圆周同胚的图形。两个纽结等价是指存在三维空间本身的一个变形，把一个变成另一个。与平面上的圆周等价的纽结称为平凡纽结（因为把未打结的绳子两头捻合得到的圈可以放在平面上）。同时这也是绳结魔术的数学道理。

如果不是考虑一条闭曲线,而是同时考虑h条闭曲线，要求它们既不自交也不互交,那么就得到h圈链环的概念。等价性的定义也与纽结的相仿。图3中是两个非平凡的（即不等价于互相分离的圆周的）双圈链环，它们彼此也不等价1。

纽结理论的基本问题是:怎样区分不等价的纽结(或链环)？它是三维拓扑学的一部分,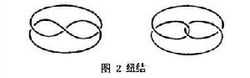因为曲线打结与链锁是三维空间所特有的现象（平面上、四维以上的空间里曲线都不会打结），而且它所研究的是闭曲线在三维空间中安放方式的差异，并不是闭曲线本身（它们都与圆周同胚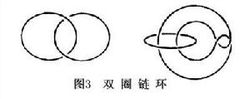，因而彼此都同胚）。

纽结的投影每个纽结,选取适当的投影方向,总可以使它在平面上的投影的自交点都只是二重交叉点；以线的虚实表现交叉的情况，就得到纽结的投影图。纽结的等价类被它的投影图所完全确定，但是等价的纽结可以有不同的投影图。图4的两个纽结是分别与图2的两个纽结等价的,它们通常称为三叶结与8字结。

纽结的不变量要证明两个纽结等价，只须用绳各作一个模型然后把一个变形成另一个。然而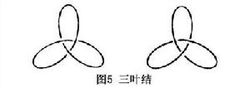如果你失败了，并不足以证明这两个纽结不等价，或许还有什么诀窍能使它们互变呢！因此，要证明两个纽结不等价，必须用不变量，即纽结的在变形下不改变的性质。

不变量之一是纽结的群，即从三维空间中挖去该纽结后所余的开集的基本群。它容易计算，有简单的步骤从该纽结的投影图来写出它的母元和关系。然而它不易鉴别,因为用母元和关系写出的两个群,没有普遍适用的办法来鉴定它们是否同构。平凡纽结的特征是，它的群是无限循环群。然而,群相同的纽结不一定等价。图5中的两个三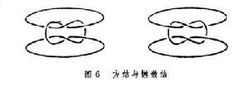叶结互为镜像，因而有相同的群，但是它们不等价。图6是两个常用的结,也是群相同而不等价。众所周知，左边的结牢靠，有方结、外科结等名称，而右边的易散，被称为懒散结。那是它们的物理性质，不是几何性质。

纽结的运算在一条绳上先后打两个结，其结果称为两个结的和（图7）。很明显,这加法满足结合律,平凡结起着零的作用。交换律可以从图8看出。全体纽结在加法运算下构成一个交换半群。就象每个正整数在乘法运算下有惟一的素因子分解一样，每个非平凡的纽结可以分解成素纽结（即不能再分解的非平凡纽结，例如三叶结与8字结）的和,而且只有一个这样的分解式。方结是三叶结与其镜像之和，而懒散结则是两个三叶结之和。

历史与现状C.F.高斯在1833年研究电动力学时引进了闭曲线之间的环绕数，这是纽结理论的基本工具之一。1880年左右出现了最早的纽结表。纽结理论后来随着代数拓扑学的发展而前进，也反过来刺激了代数拓扑学的发展。1910年M.W.德恩引进纽结的群的概念，1928年J.W.亚历山大引进了纽结的多项式这个更易处理的不变量，都是重要的进步。纽结理论是拓扑学的一个引人入胜的领域，一方面因为它研究的是看得见摸得着的丰富多彩的几何现象，有着许多问题等待人们去解决，另一方面也因为它相当奥妙,需要动用各种各样的方法,成了诸如群论、矩阵论、数论、代数几何、微分几何等众多学科与拓扑学交汇的地方。

目前，已经有了能够判断纽结的等价性的算法，可以造出一台机器，输入任意两个纽结的投影图，它都能判定它们是否等价。然而这只解决了理论上的可判定性，还不切实可行。在实际计算方面，已发明了一些新的多项式不变量，它们比亚历山大多项式包含更多的信息。

由于纽结、链环与三维、四维流形的构造和分类有深刻的联系，与奇点理论也密切相关，也由于高维纽结（n维球面在n+2维空间中安放方式）的研究的进展，纽结理论近年来引起更多人的兴趣。它也被应用于化学中大分子的空间结构的研究，例如遗传物质DNA的研究。

20世纪八十年代，jones发明了纽结多项式，为纽结理论的发展做出了进一步的推动。