[科普中国]-混循环小数

循环节不是从小数部分第一位开始的，叫混循环小数 。例如：1.2333333……、13.0984343434343……等。我们可以观察到：1.2333333……的循环节在3上面。

简介一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数叫循环小数（circulating decimal）。循环节不是从小数部分第一位开始的，叫混循环小数 。例如：1.2333333……、13.0984343434343……等。我们可以观察到：1.2333333……的循环节在3上面。

特点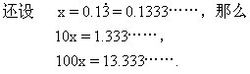最简分数a/b能化为混循环小数的充要条件是分母b既含有质因数2或5，又含有2和5以外的质因数。如：1/6,2/15等。

化分数方法描述一个混循环小数的小数部分可以化成分数：

这个分数的分子是第二个循环节以前的小数部分组成的数与小数部分中不循环部分组成的数的差。

分母的头几位数是9，末几位是0。其中9的个数与循环节中的位数相同，0的个数与不循环部分的位数相同。

举例0.13333……化为分数

分子：13-1=12

分母：循环节1位，不循环部分1位，因此是90

即0.13333……=12/90=2/15

纯循环小数简介从小数部分第一位开始的循环小数，称为纯循环小数。纯循环小数是从十分位开始循环的小数，如0.33333333...(1/3)，0.1428571428571....(1/7)等。顾名思义，纯循环小数就是在纯小数的基础上变成循环小数。

特点（1）分母只含有2或5的因数的最简分数，可以化为有限小数；

（2）分母中含有2或5以外的因数的最简分数，可以化为循环小数，但不一定是纯循环小数。

（3）若最简分数a/b的分母b只含有2和5以外的质因数（即b的质因数不包括2和5），则该分数能化为纯循环小数1。

本词条内容贡献者为:

姚远 - 副教授 - 北京邮电大学