[科普中国]-最小正周期

算法实例

函数f(x)±g(x)最小正周期的求法

定义法概念：根据周期函数和最小正周期的定义，确定所给函数的最小正周期。

例1、求函数y=|sinx|+|cosx|的最小正周期.

解:∵ =|sinx|+|cosx|

=|－sinx|+|cosx|

=|cos(x+π/2)|+|sin(x+π/2)|

=|sin(x+π/2)|+|cos(x+π/2)|

=f(x+π/2)

对定义域内的每一个x，当x增加到x+π/2时，函数值重复出现，因此函数的最小正周期是π/2.（如果f（x+T）=f（x），那么T叫做f（x）的周期）。

例2 、求函数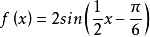的最小正周期。

解：把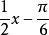看成是一个新的变量z,那么2sinz的最小正周期是2π。

由于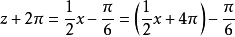。所以当自变量x增加到x+4π且必须增加到x+4π时，函数值重复出现。

∴函数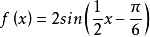的最小正周期是4π。

公式法这类题目是通过三角函数的恒等变形，转化为一个角的一种函数的形式，用公式去求，其中正余弦函数求最小正周期的公式为T=2π/|ω| ，正余切函数T=π/|ω|。

函数f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)(A≠0,ω>0）的最小正周期都是；函数f(x)=Atan(ωx+φ)和f(x)=Acot(ωx+φ)(A≠0,ω>0）的最小正周期都是，运用这一结论，可以直接求得形如y=Af(ωx+φ)(A≠0,ω>0）一类三角函数的最小正周期（这里“f”表示正弦、余弦、正切或余切函数）。

例3、求函数y=cotx－tanx的最小正周期.

解：y=1/tanx－tanx=(1－tan^2· x)/tanx=2*(1－tan^2·x)/(2tanx)=2cot2x

∴T=π/2

函数为两个三角函数相加，若角频率之比为有理数，则函数有最小正周期。

最小公倍数法设f(x)与g(x)是定义在公共集合上的两个三角周期函数，T1、T2分别是它们的周期，且T1≠T2，则f(x)±g(x)的最小正周期T1、T2的最小公倍数，分数的最小公倍数=T1,T2分子的最小公倍数/T1、T2分母的最大公约数。

求几个正弦、余弦和正切函数的最小正周期，可以先求出各个三角函数的最小正周期，然后再求期最小公倍数T,即为和函数的最小正周期2。

例4、求函数y=sin3x+cos5x的最小正周期.

解：设sin3x、cos5x的最小正周期分别为T1、T2，则T1=2π/3,T2=2π/5 ，所以y=sin3x+cos5x的最小正周期T=2π/1=2π.

例5、求y=sin3x+tan2x/5 的最小正周期.

解：∵sin3x与tan2x/5 的最小正周期是2π/3与5π/2,其最小公倍数是10π/1=10π.

∴y=sin3x+tan2x/5的最小正周期是10π.

说明：几个分数的最小公倍数，我们约定为各分数的分子的最小公倍数为分子，各分母的最大公约数为分母的分数。

图象法概念：作出函数的图象，从图象上直观地得出所求的最小正周期。

例6、求y=|sinx|的最小正周期.

解：由y=|sinx|的图象

可知y=|sinx|的周期T=π.

例7、求下函数的最小正周期。

（1）

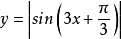
（2）

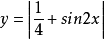
解：（1）先作出函数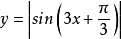的图象（见图1）

观察图象，易得所求的周期为T=π/3。

（2）先作出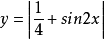的图象（见图2）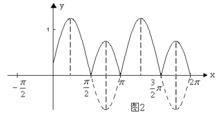

观察图象，易得所求的周期为T=π。

恒等变换法概念：通过对所给函数式进行恒等变换，使其转化为简单的情形，再运用定义法、公式法或图象法等求出其最小正周期3。

(1) f(x)=sin(x+π/3)cos(x-π/3)

(2) f(x)=sin6x+cos6x

(3) f(x)=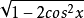

解 (1)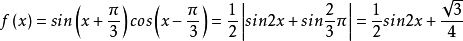

∴最小正周期为T= π

(2) f(x)=sin6x+cos6x

=(sin2x+cos2x)(sin4x-sin2xcos2x+cos4x)

=(sin4x-sin2xcos2x+cos4x)

=(sin2x+cos2x)2-3sin2xcos2x

=1-3/4sin2x

=5/8+3/8cos4x

∴最小正周期为T=π/2

(3)

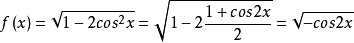
它与－cos2x的周期相同，故得 f(x)的最小正周期为T=π

补充问题函数f(x)=sin2x-4sin³xcosx(x∈R)的最小正周期为（ B ）

A.π/4 B.π/2 C.π D.2π