[科普中国]-曲率

定义

弧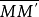 的切线转角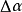 与该弧长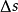 之比的绝对值称作该弧的平均曲率，记作

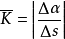
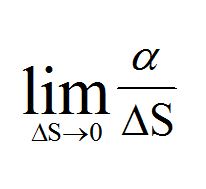
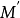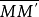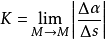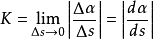当 沿曲线L趋向于M时，若弧 的平均曲率的极限存在，则称此极限为曲线L在点M处的曲率，记作K，即 或 。1

计算公式设曲线的直接坐标方程为y=f（x），且y=f（x）具有二阶导数，曲线在点M处的切线的斜率为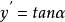 ,所以

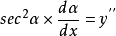
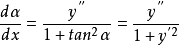
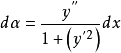又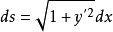 ,故曲线L在M点处的曲率为

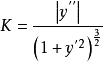设曲线是由参数方程 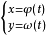给出，利用参数方程求导法可得

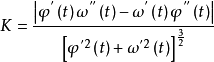
曲率圆与曲率半径曲线上点M处的曲率的倒数，称作曲线在这点处的曲率半径，记作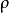 ,则

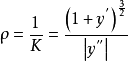在点M处曲线的法线的某一侧上取一点D，使 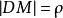，并以D为圆心，以 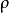为半径作圆。把这个圆称作曲线在点M处的曲率圆，把圆心D称做曲线在M处的曲率中心。

曲率圆具有以下性质：

（1）曲率圆与曲线在点M处有共同的切线和曲率；

（2）在点M邻近与曲线有相同的凹向；

因此，在实际工程设计问题中，常用曲率圆在点M邻近的一段圆弧来近似代替曲线弧，以使问题简化。2

意义曲率是几何体不平坦程度的一种衡量。平坦对不同的几何体有不同的意义。

本文考虑基本的情况，欧几里得空间中的曲线和曲面的曲率。一般意义下的曲率，请参照曲率张量。

在动力学中，一般的，一个物体相对于另一个物体做变速运动时也会产生曲率。这是关于时空扭曲造成的。结合广义相对论的等效原理，变速运动的物体可以看成处于引力场当中，因而产生曲率。

按照广义相对论的解释，在引力场中，时空的性质是由物体的“质量”分布决定的，物体“质量”的分布状况使时空性质变得不均匀，引起了时空的弯曲。因为一个物体有质量就会对时空造成弯曲，而你可以认为有了速度，有质量的物体变得更重了，时空弯曲的曲率就更大了。

在物理中，曲率通常通过法向加速度（向心加速度）来求，具体请参见法向加速度。