[科普中国]-梯度

定义

设二元函数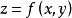 在平面区域D上具有一阶连续偏导数，则对于每一个点P（x，y）都可定出一个向量 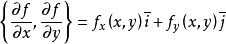,该函数就称为函数 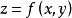在点P（x，y）的梯度，记作gradf（x，y）或 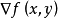,即有：

gradf（x，y）= =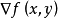

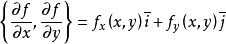
其中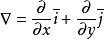 称为（二维的）向量微分算子或Nabla算子， 。

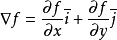设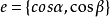 是方向l上的单位向量，则

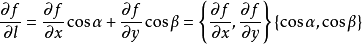
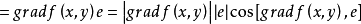
由于当方向l与梯度方向一致时，有

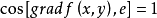
所以当l与梯度方向一致时,方向导数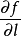 有最大值，且最大值为梯度的模，即

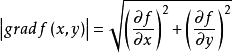
因此说，函数在一点沿梯度方向的变化率最大，最大值为该梯度的模。1

推广梯度的概念可以推广到三元函数的情形。

设三元函数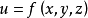 在空间区域G内具有一阶连续偏导数，点 ，称向量

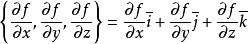
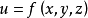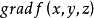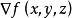为函数 在点P的梯度，记为 或 ，即

==

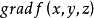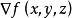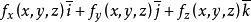
其中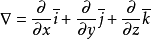称为（三维的）向量微分算子或Nabla算子，。

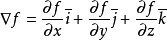同样，该梯度方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。2

应用设体系中某处的物理参数(如温度、速度、浓度等)为w，在与其垂直距离的dy处该参数为w+dw，则称为该物理参数的梯度，也即该物理参数的变化率。如果参数为速度、浓度、温度或空间，则分别称为速度梯度、浓度梯度、温度梯度或空间梯度。其中温度梯度在直角坐标系下的表达式如右图。2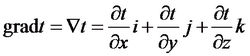

在向量微积分中，标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。更严格的说，从欧几里得空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。在这个意义上，梯度是雅可比矩阵的特殊情况。

在单变量的实值函数的情况，梯度只是导数，或者，对于一个线性函数，也就是线的斜率。

梯度一词有时用于斜度，也就是一个曲面沿着给定方向的倾斜程度。可以通过取向量梯度和所研究的方向的点积来得到斜度。梯度的数值有时也被称为梯度。