[科普中国]-置信区间

理论描述

对于一组给定的样本数据，其平均值为μ，标准偏差为σ，则其整体数据的平均值的100(1-α)%置信区间为(μ-Ζα/2σ , μ+Ζα/2σ) ，其中α为非置信水平在正态分布内的覆盖面积 ，Ζα/2即为对应的标准分数。1

随机区间

对于一组给定的数据，定义 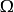为观测对象，W为所有可能的观测结果，X为实际上的观测值，那么X实际上是一个定义在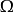上，值域在W 上的随机变量。这时，置信区间的定义是一对函数u(.) 以及v(.) ，也就是说，对于某个观测值X=x，其置信区间为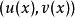。实际上，若真实值为w，那么置信水平就是概率c：

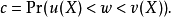其中U=u(X)和 V=v(X)都是统计量（即可观测的随机变量），而置信区间因此也是一个随机区间：(U,V)。

公式Pr(c1