基本概念
对实数x>-1,1
在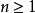 时,有
时,有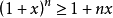 成立;
成立;
在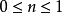 时,有
时,有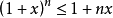 成立。
成立。
可以看到等号成立当且仅当n = 0,1,或x = 0时。
伯努利不等式经常用作证明其他不等式的关键步骤。
伯努利不等式的一般式为
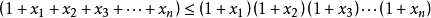
(对于任意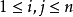 都有
都有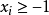 且
且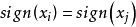 ,即所有
,即所有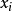 同号且大于等于-1) 当且仅当n=1时等号成立
同号且大于等于-1) 当且仅当n=1时等号成立
证明设x>-1,且x≠0,n是不小于2的整数,则(1+x)^n≥1+nx。2
证明:
先证明对所有正整数不等式成立。用数学归纳法:
当n=1,上个式子成立,
设对n-1,有:
(1+x)^(n-1)>=1+(n-1)x成立。
则
(1+x)^n
=(1+x)^(n-1)(1+x)
>=[1+(n-1)x](1+x)
=1+(n-1)x+x+(n-1)x^2=1+nx+nx^2-x^2
>=1+nx
就是对一切的自然数,当
x>=-1,有
(1+x)^n>=1+nx
下面把伯努利不等式推广到实数幂形式:
若r ≤0或r ≥ 1,有(1+x)^r ≥ 1 + rx
若0 ≤ r ≤ 1,有(1+x)^r ≤ 1 + rx
这个不等式可以直接通过微分进行证明,方法如下:
如果r=0,1,则结论是显然的
如果r≠0,1,作辅助函数f(x)=(1+x)^r-(1+rx), 那么f'(x)=r*(1+x)^(r-1)-r, 则f'(x)=0 x=0;
下面分情况讨论:
1. 0 0,f'(x) 0。严格递增,因此f(x)在x = 0处取最大值0,故得(1+x)^r ≤ 1+rx。
2. r 1,则对于x > 0,f'(x) > 0;对于 − 1
证毕。
相关不等式下述不等式从另一边估计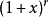 :对任意
:对任意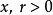 ,都有
,都有
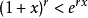 。
。
我们知道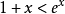 ( x>0),因此这个不等式是平凡的。
( x>0),因此这个不等式是平凡的。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国