[科普中国]-泊松过程

定义

Poisson过程（Poisson process，大陆译泊松过程、普阿松过程等，台译卜瓦松过程、布瓦松过程、布阿松过程、波以松过程、卜氏过程等），是以法国数学家泊松（1781 - 1840）的名字命名的。泊松过程是随机过程的一种，是以事件的发生时间来定义的。我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程，如果它满足以下条件：

在两个互斥（不重叠）的区间内所发生的事件的数目是互相独立的随机变量。

在区间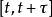内发生的事件的数目的概率分布为：

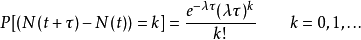
其中λ是一个正数，是固定的参数，通常称为抵达率（arrival rate）或强度（intensity）。所以，如果给定在时间区间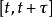之中事件发生的数目，则随机变数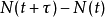呈现泊松分布，其参数为。

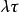更一般地来说，一个泊松过程是在每个有界的时间区间或在某个空间（例如：一个欧几里得平面或三维的欧几里得空间）中的每一个有界的区域，赋予一个随机的事件数，使得

在一个时间区间或空间区域内的事件数，和另一个互斥（不重叠）的时间区间或空间区域内的事件数，这两个随机变数是独立的。

在每一个时间区间或空间区域内的事件数是一个随机变数，遵循泊松分布。（技术上而言，更精确地来说，每一个具有有限测度的集合，都被赋予一个泊松分布的随机变数。）

泊松过程是莱维过程（Lévy process）中最有名的过程之一。时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。一个时间齐次、一维的泊松过程是一个纯出生过程，是一个出生-死亡过程的最简单例子。

泊松简介泊松，法国数学家，1781年6月21日生于法国卢瓦

雷省的皮蒂维耶，1840年4月25日卒于法国索镇。

1798年入巴黎综合理工科学校深造。在毕业时，因优秀的研究论文而被指定为讲师。受到P.-S.拉普拉斯、J.-L.拉格朗日的赏识。1800年毕业后留校任教，1802年任副教授,1806年接替J.-B.-J.傅里叶任该校教授。1808年任法国经度局天文学家,1809年任巴黎理学院力学教授。1812年当选为巴黎科学院院士。

泊松的科学生涯开始于研究微分方程及其在摆的运动和声学理论中的应用。他工作的特色是应用数学方法研究各类力学和物理问题，并由此得到数学上的发现。他对积分理论、行星运动理论、热物理、弹性理论、电磁理论、位势理论和概率论都有重要贡献。

性质考虑一个泊松过程，我们将第一个事件到达的时间记为T1。此外，对于n>1，以Tn记在第n-1个事件与第n个事件之间用去的时间。序列{Tn,n=1,2,...}称为到达间隔时间列。

Tn(n=1,2,...)是独立同分布的指数随机变量，具有均值1/λ。

名词解释泊松过程用数学语言说，满足下列三条件的随机过程X={X(t),t≥0}叫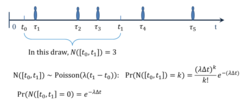做泊松过程。

①P(X(0)=0)=1。

②不相交区间上增量相互独立，即对一切0≤t1