[科普中国]-调和级数

历史

早在14世纪，尼克尔·奥里斯姆已经证明调和级数发散，但知道的人不多。17世纪时，皮耶特罗·曼戈里、约翰·伯努利和雅各布·伯努利完成了全部证明工作。1

调和序列历来很受建筑师重视；这一点在巴洛克时期尤其明显。当时建筑师在建造教堂和宫殿时，运用调和序列为楼面布置和建筑物高度建立比例，并使室内外的建筑细节间呈现和谐的联系。

发散性比较审敛法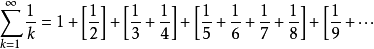

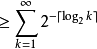
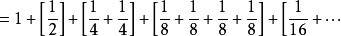
因此该级数发散。2

积分判别法通过将调和级数的和与一个瑕积分作比较可证此级数发散。考虑右图中长方形的排列。每个长方形宽1个单位、高1/n个单位（换句话说，每个长方形的面积都是1/n），所以所有长方形的总面积就是调和级数的和： 矩形面积和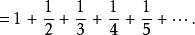：而曲线y=1/x以下、从1到正无穷部分的面积由以下瑕积分给出： 曲线下面积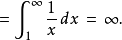：由于这一部分面积真包含于（换言之，小于）长方形总面积，长方形的总面积也必定趋于无穷。更准确地说，这证明了：

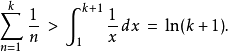
这个方法的拓展即积分判别法。

反证法假设调和级数收敛 , 则：

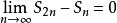
但与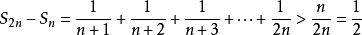矛盾，故假设不真，即调和级数发散。

发散率调和级数发散的速度非常缓慢。举例来说，调和序列前10项的和还不足100。这是因为调和数列的部分和呈对数增长。特别地，3

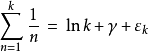
其中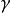是欧拉-马歇罗尼常数，而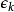约等于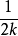，并且随着 k趋于正无穷而趋于 0。这个结果由欧拉给出。

部分和调和级数的第n个部分和为：

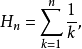
也叫作第n个调和数。

第n个调和数与n的自然对数的差值（即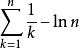）收敛于欧拉-马歇罗尼常数。

两个不同的调和数之间的差值永远不是整数。

除了n=1时以外，没有任何一个调和数是整数。

定义很早就有数学家研究，比如中世纪后期的数学家Oresme在1360年就证明了这个级数是发散的。他的方法很简单：

1 +1/2+1/3 +1/4 + 1/5+ 1/6+1/7+1/8 +...

1/2+1/2+(1/4+1/4)+(1/8+1/8+1/8+1/8)+...

注意后一个级数每一项对应的分数都小于调和级数中每一项，而且后面级数的括号中的数值和都为1/2，这样的1/2有无穷多个，所以后一个级数是趋向无穷大的，进而调和级数也是发散的。

从更广泛的意义上讲，如果An是全部不为0的等差数列，则1/An就称为调和数列，求和所得即为调和级数，易得，所有调和级数都是发散于无穷的。

推导随后很长一段时间，人们无法使用公式去逼近调和级数，直到无穷级数理论逐步成熟。1665年牛顿在他的著名著作《流数法》中推导出第一个幂级数：

ln(1+x) = x - x^2/2 + x^3/3 - ...

Euler(欧拉)在1734年，利用Newton的成果，首先获得了调和级数有限多项和的值。结果是：

1+1/2+1/3+1/4+...+1/n= ln(n+1)+r(r为常量)

他的证明是这样的：

根据Newton的幂级数有：

ln(1+1/x) = 1/x - 1/2x^2 + 1/3x^3 - ...

于是：

1/x = ln((x+1)/x) + 1/2x^2 - 1/3x^3 + ...

代入x=1,2,...,n，就给出：

1/1 = ln(2) + 1/2 - 1/3 + 1/4 -1/5 + ...

1/2 = ln(3/2) + 1/2*4 - 1/3*8 + 1/4*16 - ...

......

1/n = ln((n+1)/n) + 1/2n^2 - 1/3n^3 + ...

相加，就得到：

1+1/2+1/3+1/4+...1/n = ln(n+1) + 1/2*(1+1/4+1/9+...+1/n^2) - 1/3*(1+1/8+1/27+...+1/n^3) + ......

后面那一串和都是收敛的，我们可以定义

1+1/2+1/3+1/4+...1/n = ln(n+1) + r

Euler近似地计算了r的值，约为0.5772156649。这个数字就是后来称作的欧拉常数。

欧拉常数是个无理数，因为自然数倒数和虽然是发散的但是它的每一项都是有理数，而ln(n)确是个无理数，一个有理数减去无理数必然是无理数因为

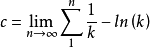
自然数倒数和逼近公式

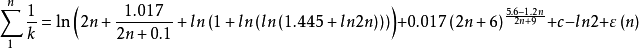c为欧拉常数

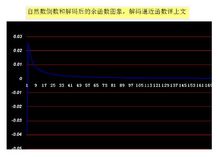
解码函数比原函数偏小，函数在n=1 时误差为-0.0382064988721671，n（2,7）时误差为0.0257360642441862~0.0106247817461118，n>=7时误差为0.00942087240133116左右，n>=70 时0.000998481033276377左右n特别大时逐渐时趋于0。误差就是余函数ε（n）的取值。解码逼近函数比原函数稍偏小，误差最大区间是1~7之间。

以下是余函数ε（n）的图像。

拓延调和级数有以下性质：

f(n)-f(n-1)=1/n

我们可以寻找一个函数G(x)，他在定义域内此性质恒成立，且其经过所有的调和级数。

我们暂定其定义域为（0，）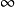

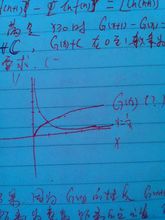
则G（0）=G(1)-1/1=0

G(n+1)-G(n)=1/(n+1) (n>=0) 恒成立

G(x)为连续的凸函数（重要）

则有无数曲线即有无数函数满足以上要求。我们将其中为凸函数的一个求出，作为调和级数在实数上的合理拓延。

以下求解过程在定义域内完成，不作赘述。

G(x+1)-G(x)=1/(x+1) ①

G(x+1+m)-G(x+m)=1/(x+1+m) ②

②-①在除以m得

[G(x+1+m)-G(x+1)]/m - [G(x+m)-G(x)]/m = 1/(x+1) - 1/(x+1+m)

m趋于无穷小时，g(x)表示G(x)的导数 得

g(x+1)-g(x)=-1/(x+1)^2 ③

因为G(x)为凸函数，所以有以下性质

1/(x+1)1/2,而调和级数的第一项是1，也就是说调和级数的和要想达到51那么它需要有2的100次方那个多项才可以。而2的100次方这个项是一个大到我们能够处理范围以外的数字，在计算机元科学领域，这属于一个不可解的数。

p-级数在P>1的时候是收敛的，也就是说对于任意ε>0,n的1+ε次方的倒数这个级数是收敛的,在我们直观上看来,好像调和级数下面的n只要大了一小点,或者说调和级数的每一项只要小一小点点,那么这个级数就是收敛的了,但是事实上并不是这样sin1/n这个级数的发散的,但是在1/n>0的时候,sin1/n0 n=1

S>1 n=2

S>2 n=4

S>3 n=11

S>4 n=31

S>5 n=83

S>6 n=227

S>7 n=616

S>8 n=1674

S>9 n=4550

S>10 n=12367

S>11 n=33617

S>12 n=91380

S>13 n=248397

S>14 n=675214

S>15 n=1835421

......

计算机程序（C）：

注意：本程序由于浮点误差，当S>=16时不保证结果准确；但算法是正确的，仅供参考。

#include

int main()

{

int k,i=0;

double tot=0;

scanf("%d",&k);

while(tot