[科普中国]-不动点

举例

例如，定义在实数上的函数f，1

f(x)=x2-3x+4，

则2是函数f的一个不动点，因为 f(2)=2。

也不是每一个函数都具有不动点。例如定义在实数上的函数f(x)=x+1就没有不动点。因为对于任意的实数，x永远不会等于x+1。用画图的话来说，不动点意味着点 (x,f(x))在直线y=x上，或者换句话说，函数f的图像与那根直线有共点。上例 f(x)=x+1的情况是，这个函数的图像与那根直线是一对平行线。

在函数的有限次迭代之后回到相同值的点叫做周期点；不动点是周期等于 1 的周期点。

原理不动点原理是数学上一个重要的原理，也叫压缩映像原理或巴拿赫（Banach）不动点定理，完整的表达：完备的度量空间上，到自身的一个压缩映射存在唯一的不动点。用初等数学可以这么理解：连续映射f的定义域包含值域，则存在一个x使得f(x)=x。1

不动点的概念可以推广到一般的拓扑空间上。 假设X是拓扑空间， f:X→X是一个连续映射， 且存在x∈X， 使得f(x)=x, 就称x是不动点。

数学应用1 利用f(x)的不动点解方程（牛顿切线法）

2 利用f(x)的不动点求函数或多项式的解析式

3 利用f(x)的不动点讨论n-周期点问题

4 求解数列问题（求解一阶递归数列的通项公式）

5 求解一阶递归数列的极限

这是利用不动点开立方（牛顿切线法）的例子

开方：

公式：X(n+1）=Xn+（A/Xn^2-Xn）1/3设A=5，开3次方

5介于1^3至2^3之间（1的3次方=1，2的3次方=8）

X_0可以取1.1，1.2，1.3，1.4，1.5，1.6，1.7，1.8，1.9，2.0都可以。例如我们取2.0.按照公式：

第一步：X1={2.0+[5/(2.0^2-2.0]1/3=1.7.}。即5/2×2=1.25，1.25-2=-0.75，0.75×1/3=0.25，输入值大于输出值，负反馈

2-0.25=1.75，取2位数值,即1.7。

第二步：X2={1.7+[5/(1.7^2-1.7]1/3=1.71}.。

即5/1.7×1.7=1.73010，1.73-1.7=0.03，0.03×1/3=0.01，输入值小于输出值正反馈

1.7+0.01=1.71。取3位数，比前面多取一位数。

第三步：X3={1.71+[5/(1.71^2-1.71]1/3=1.709}输入值大于输出值，负反馈

第四步：X4={1.709+[5/(1.709^2-1.709]1/3=1.7099}.输入值小于输出值正反馈

这种方法可以自动调节，第一步与第三步取值偏大，但是计算出来以后输出值会自动转小；第二步，第四步输入值偏小，输出值自动转大。X_4=1.7099。

当然也可以取1.1,1.2,1.3,...1.8,1.9中的任何一个。

实际应用取一个浅盒和一张纸，纸恰好盖住盒内的底面。可想而知此时纸上的每个点与正在它下面的盒底上的那些点配成对。把这张纸拿起来，随机地揉成一个小球，再把小球扔进盒里。拓扑学家已经证明，不管小球是怎样揉成的，也不管它落在盒底的什么地方，在揉成小球的纸上至少有一个这样的点，它恰好处在它盒底原来配对点的正上方。

通过具体找到这个点，就能说明这个问题了。

纸被揉成球以后，看它投到纸盒底部的影子。纸盒底部的影子区域肯定比纸盒底要小。那么，就取纸盒底部的在影子内的那个部分，它肯定对应于纸团里面的某一小团部分。（因为整个底板对应于整个纸团，那么底板的一部分就肯定对应于一部分纸团）

假如去掉纸团的其他部分，那一小团部分同样可以在纸盒底面投影，而且投影肯定比刚才的大投影小，而且在它之内。（因为它是在整个纸团之内）。那么，取这一小片投影（注意这片影子肯定是连续的不会断开，因为纸没有撕裂），当它再往纸团里对应的时候，肯定对应于其中更小的一团。我们再次把多余的纸去掉。

就是说：

整个纸盒对应于纸团

纸盒【在纸团投影内的部分】对应于纸团内的一小块

纸盒【一小块的投影的部分】对应于刚才那一小块内的更小一块

纸盒【更小块投影的部分】对应于更小块中的更更小一块

…………………………

不断地去掉纸无限次，最后纸团只剩下了一个点，它的投影就对应于纸盒的一个点。

吸引不动点函数f的吸引不动点是f的不动点x0使得，对在足够接近x0的定义域中的任何x值而言，迭代函数序列

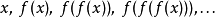
收敛于x0。如何接近才是“足够接近”有时是个微妙的问题。

自然余弦函数（自然意味着使用弧度而非角度）有精确的一个吸引不动点。在这种情况下，“足够接近”根本不是严格标准 -- 为了展示这个情况，在计算器上开始于任何实数并重复按“cos”键。它会快速的收敛于大约 0.73908513，这就是不动点。这是余弦函数和线 y=x 在图上的交叉点。

不是所有不动点都是吸引的：例如，x=0是函数 f(x)=2x 的不动点，但是这个函数对非零任意值的迭代快速的发散。

吸引不动点是更广泛的数学概念吸引子的特殊情况。

吸引不动点被称为稳定不动点如果它也是李雅普诺夫稳定性的。

一个不动点被称为是中立稳定不动点如果它是李雅普诺夫稳定性的但不是吸引的。二阶齐次线性微分方程的中心点是中立稳定不动点的例子。

定理在数学的不同部分有很多定理保证函数、在一定的条件下，必定有一个或者更多的不动点。这些在最基本的定性结果当中，那些普遍性应用的不动点定理是非常具有价值的洞察。2