[科普中国]-插值

在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。1

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

插值：用来填充图像变换时像素之间的空隙。

发展历史早在6世纪，中国的刘焯已将等距二次插值用于天文计算。

17世纪之后，I.牛顿，J.-L.拉格朗日分别讨论了等距和非等距的一般插值公式。在近代，插值法仍然是数据处理和编制函数表的常用工具，又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础，许多求解计算公式都是以插值为基础导出的。

定义给定 n个离散数据点（称为节点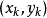） ，k=1,2,...,n。对于 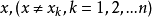，求 x所对应的 y的值称为内插。2

f(x)为定义在区间 [a,b]上的函数。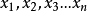为[a,b]上n个互不相同的点， G为给定的某一函数类。若G上有函数 g(x)满足：

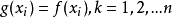
则称g(x)为f(x)关于节点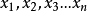在 G上的插值函数。

主要内涵插值问题的提法是：假定区间[a,b]上的实值函数f(x)在该区间上 n+1个互不相同点x0,x1,……,xn 处的值是f (x0),……f(xn)，要求估算f(x)在[a,b]中某点x*的值。基本思路是，找到一个函数P(x)，在x0,x1,……,xn的节点上与f(x)函数值相同(有时，甚至一阶导数值也相同)，用P(x*)的值作为函数f(x*)的近似。

其通常的做法是：在事先选定的一个由简单函数构成的有n+1个参数C0，C1，……Cn的函数类Φ(C0,C1,……Cn)中求出满足条件P(xi)=f(xi)(i=0,1,…… n)的函数P(x)，并以P()作为f()的估值。此处f(x)称为被插值函数，x0,x1,……,xn称为插值结(节)点，Φ(C0,C1,……Cn)称为插值函数类，上面等式称为插值条件，Φ(C0,C1,……Cn)中满足上式的函数称为插值函数，R(x)= f(x)－P(x)称为插值余项。当估算点属于包含x0,x1,……,xn的最小闭区间时，相应的插值称为内插，否则称为外插。

基本类型多项式这是最常见的一种函数插值。在一般插值问题中，若选取Φ为n次多项式类，由插值条件可以唯一确定一个n次插值多项式满足上述条件。从几何上看可以理解为：已知平面上n+1个不同点，要寻找一条n次多项式曲线通过这些点。插值多项式一般有两种常见的表达形式，一个是拉格朗日插值多项式，另一个是牛顿插值多项式。1

埃尔米特对于函数f(x)，常常不仅知道它在一些点的函数值，而且还知道它在这些点的导数值。这时的插值函数P(x)，自然不仅要求在这些点等于f(x)的函数值，而且要求P(x)的导数在这些点也等于f(x)的导数值。这就是埃尔米特插值问题，也称带导数的插值问题。从几何上看，这种插值要寻求的多项式曲线不仅要通过平面上的已知点组，而且在这些点（或者其中一部分）与原曲线“密切”，即它们有相同的斜率。可见埃尔米特插值多项式比起一般多项式插值有较高的光滑逼近要求。

分段分段插值与样条插值

为了避免高次插值可能出现的大幅度波动现象，在实际应用中通常采用分段低次插值来提高近似程度，比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数，但它们的总体光滑性较差。为了克服这一缺点，一种全局化的分段插值方法——三次样条插值成为比较理想的工具。见样条函数。

三角函数当被插函数是以2π为周期的函数时，通常用n阶三角多项式作为插值函数，并通过高斯三角插值表出。

辛克插值 在抽样信号中我们以使用辛克插值，它可以由样品值完美地重建原始信号。著名的抽样定理表述，对于正确的抽样信号s(t)，原始信号可以由抽样值sk进行重建，其公式为：

s(t) = ∑ sksincπ(t-tk) (注：k为下标)

这里sk代表在时间tk=t0+k*T时的抽样值，T是抽样时间，它的倒数1/T叫做抽样频率。此公式表示，已知在规则分布的区间中的抽样值sk，我们就可以根据辛克函数先测出抽样值，然后将它们相加，这样计算出任意时间t上的值。

编程使用matlab中使用插值函数

插值函数(the function of interpolation )

interp1

调用函数的格式(Syntax)

yi = interp1(x,Y,xi)

yi = interp1(Y,xi)

yi = interp1(x,Y,xi,method)

yi = interp1(x,Y,xi,method,'extrap')

yi = interp1(x,Y,xi,method,extrapval)

pp = interp1(x,Y,method,'pp')

调用格式说明(Description)

yi = interp1(x,Y,xi) 返回矢量X和Y决定的根据输入的节点xi时对应的y的值.矢量Y是矢量X的一个函数映射.

如果Y是一个矩阵,那么插值结果是一个对应的矩阵.

[===================================================

yi = interp1(x,Y,xi) returns vector yi containing elements corresponding to the elements of xi and determined by interpolation within vectors x and Y. The vector x specifies the points at which the data Y is given. If Y is a matrix, then the interpolation is performed for each column of Y and yi is length(xi)-by-size(Y,2).

===================================================]

yi = interp1(x,Y,xi,method)插值中可以使用的方法:

|| ||

[====================================================

yi = interp1(x,Y,xi,method) interpolates using alternative methods:

methodDescription

nearestNearest neighbor interpolation

linearLinear interpolation (default)

splinesplineCubic spline interpolation

pchipPiecewise cubic Hermite interpolation

cubic(Same as 'pchip')

v5cubicCubic interpolation used in MATLAB 5

======================================================]

简单程序示例

>>x=[0.0 0.1 0.195 0.3 0.401 0.5];

>>y=[0.39849 0.39695 0.39142 0.38138 0.36812 0.35206];

>>plot(x,y);

>>T=interp1(x,y,.25,'linear') %线性插值

(返回结果T=0.3862)

>> T=interp1(x,y,.25,'nearest') % 两点插值

(返回结果T=0.3814)

>>T=interp1(x,y,.25,'spline') % 三次样条插值

(返回结果T =0.3867)

>>T=interp1(x,y,.25,'cubic') %三次插值

(返回结果T =0.3867)

本词条内容贡献者为:

尚轶伦 - 副教授 - 同济大学数学科学学院