定义
微分流形M上外形式丛的一个光滑截面.设ω:M→Λ(TM),若对于外形式丛的丛射影π,满足π°ω=id,则称ω为M上的微分形式.
r次外形式丛的光滑截面称为r次微分形式,简称r形式.微分r形式全体构成的空间记为E(M),E(M)是C(M)模.因此,M上微分r形式是光滑的反对称r阶协变张量场.微分形式全体构成的空间为
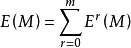 设β∈E(M),(U,y1,…,yn)为M上某点处的区图,则微分k形式β局部地可表示为
设β∈E(M),(U,y1,…,yn)为M上某点处的区图,则微分k形式β局部地可表示为
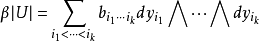 其中bi1…ik是U上的C函数.
其中bi1…ik是U上的C函数.
E(M)关于外积有一个代数结构,设ω,φ∈E(M),c为常数,可以定义ω+φ,cω,ω∧φ,f∧ω(f是0形式),从而使E(M)在外积之下构成一个分次代数.2
微分形式是微分几何学中最基本的概念。 我们首先以n维欧氏空间Rⁿ为例, 来解释微分形式。 设 是欧氏空间坐标。 在这个空间中, 我们有自然的度量, 即欧几里得度量, 它的微分表达式为
是欧氏空间坐标。 在这个空间中, 我们有自然的度量, 即欧几里得度量, 它的微分表达式为
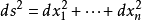 。 这里
。 这里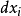 是传统的一阶微分。而
是传统的一阶微分。而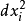 指的是
指的是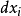 和它自己的在域R上的张量积。类似地,ds是无穷小向量dr的模长,而
和它自己的在域R上的张量积。类似地,ds是无穷小向量dr的模长,而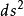 是ds和自己在域R上的张量积。
是ds和自己在域R上的张量积。
把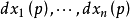 作为基向量,其中,p为
作为基向量,其中,p为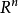 中的一个点,以实常数为系数,可以生成域R上的一个n维的向量空间, 称为
中的一个点,以实常数为系数,可以生成域R上的一个n维的向量空间, 称为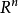 在点p的余切空间,在线性同构的意义下,它就是
在点p的余切空间,在线性同构的意义下,它就是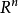 自己而已;而如果把系数由常数换成点p所在的开邻域上的实值函数,则上述的n个基向量可以生成函数环上的一个n秩的模,叫做一阶外微分形式模。在代数几何中,这个模是很常用的。
自己而已;而如果把系数由常数换成点p所在的开邻域上的实值函数,则上述的n个基向量可以生成函数环上的一个n秩的模,叫做一阶外微分形式模。在代数几何中,这个模是很常用的。
另一方面, 对一个n维向量空间V, 假设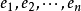 是基向量. 我们可以定义r次外积空间, 这个空间由以下形式的外积(有时也称楔积)作为基元素生成:
是基向量. 我们可以定义r次外积空间, 这个空间由以下形式的外积(有时也称楔积)作为基元素生成: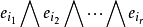 , 这里
, 这里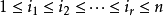 。
。
今取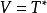 , 则
, 则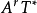 中的元素称为r次微分形式, 它可以写成基元素
中的元素称为r次微分形式, 它可以写成基元素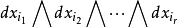 的线性组合。 这里每个基元素前的系数可以视作坐标
的线性组合。 这里每个基元素前的系数可以视作坐标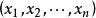 的函数。
的函数。
微分形式的概念也可以从欧氏空间推广到微分流形上。所有微分形式放在一起构成一个外代数。
性质微分形式的一个优点就是能做外微分 运算。 比如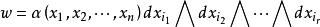 是一个r次微分形式, 那么
是一个r次微分形式, 那么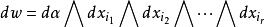 。这就把一个r次微分形式映到了r+1次微分形式。换言之,我们有映射d:
。这就把一个r次微分形式映到了r+1次微分形式。换言之,我们有映射d: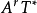 →
→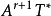 . 这个映射称为外微分。
. 这个映射称为外微分。
易知两次外微分的复合等于零, 即dd=0,即poincare(庞加莱)引理. 一个微分形式ω如果满足dω=0, 我们就称其为闭形式。 如果存在另一微分形式γ, 使得ω=dγ, 我们就称其为恰当形式。 利用dd=0这一条件,我们就得到所谓的DeRham复形, 由这个复形,就导出了所谓的DeRham上同调, 它就是闭形式生成的向量空间商掉恰当形式以后得到的商空间。
此外, 外微分运算还满足牛顿-莱布尼兹公式, 即对区域边界某外微分的积分等于对区域内该外微分的微分的积分。是高斯公式,斯托克斯公式的概括和总结,是单变量微积分中牛顿-莱布尼兹公式在多变量中的推广。
斯托克斯定理利用外微分和积分运算, 我们可以得到著名的斯托克斯定理。 它是说一个恰当形式ω=dγ在定义域M上的积分,就等于γ在M的边界上的积分。这个定理有很多特殊情况, 都是经典微积分理论中的重要公式, 比如牛顿莱布尼兹公式, 高斯公式, 格林公式 等等。
斯托克斯定理表明, 外微分算子d和拓扑图形的边缘算子是相伴的。 这暗示了微分分析和拓扑学之间的微妙联系。
例子取平面上的一阶微分ω=Pdx+Qdy. 那么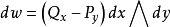 , 这里
, 这里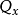 是Q关于x的偏导数,其余类似。
是Q关于x的偏导数,其余类似。
此时的斯托克斯公式就是格林公式, 即线积分可以转化为面积分。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国