[科普中国]-局部域

定义

设F为非阿基米德局部域，而为其绝对值。关键在下述对象：

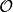闭单位球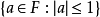：，或其整数环，这是个紧集。

整数环里的单位元：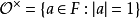

开单位球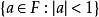：，这同时是其整数环里唯一的极大理想，也记作。

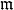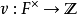上述对象与赋值环的构造相呼应；事实上，可证明必存在实数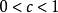及离散赋值，使得

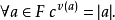
可取唯一的c使得v为满射，称之为正规化赋值。

从此引出非阿基米德局部域的另一个等价定义：一个域 F，带离散赋值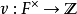，使得F成为完备的拓扑域，而且剩余域有限。

这类局部域的行为可由局部类域论描述。

分类局部域的完整分类如次：

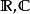。这些是阿基米德局部域。

p进数域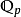的有限扩张。这些是特征为零的非阿基米德局部域。

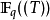的有限扩张（其中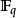表有q个元素的有限域）。这些是特征非零的非阿基米德局部域。