[科普中国]-二元运算

常见二元运算数的二元运算

a+b a加b

a-b a减b

a x b a与b相乘

ab a与b相乘

a/b a除以b

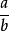a除以b

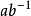a除以b 2

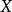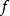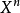集合的二元运算定义1 设 是一个集合，且 是一个从 到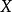 的映射。于是称 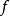为集合 X 中的n 元运算。称整数 n 为运算的阶。对

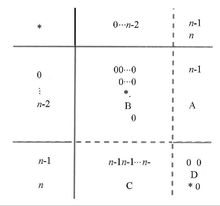
于n=2 来说，称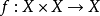 为二元运算。

定义2 设A为集合，如果f是A×A到A的代数运算，则称f是A上的一个二元运算，也称作集合A对于代数运算f来说是封闭的3。

矩阵的二元运算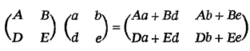

矩阵代数，特别是矩阵的乘法规则，归功于著名的英国代数学家凯利。他创立了特殊型式的超复数。矩阵的乘法可推广到更高阶矩阵。但要注意，要使乘法能进行，第一个矩阵的列数应与第二个矩阵的行数相同。凯利的规则(通常称为行乘列法则)给出了mXn矩阵与nXk矩阵的乘积4。

因为有些2×2矩阵或n×行矩阵没有逆阵，所以这种矩阵的有些集合关于乘法不是群。还有，虽然矩阵乘法总满足结合律，但在矩阵集上并不一定满足交换律。这就使得矩阵的乘法系统可以作为乘法不满足交换律的一些现代抽象代数结构的模型。由于方阵并非都是可逆的，故在矩阵的乘法系统中，不能将除法作为二元运算来看待。 凯利的矩阵代数还包括对“数乘"和加法的定义。数乘是一个一元运算，加法是矩阵的二元运算。数与矩阵相乘，就是将矩阵的每个元素都乘上该数。行数和列数分别相同的两个矩阵可以相加，只要把相应元素相加，其和是有同样的行数和列数的矩阵4。

二元运算的性质定义1 设“⊙”是非空集合A上的二元运算，如果对任意的a、b、c∈A，有(a⊙b)⊙c=a⊙(b⊙c)，则称运算“⊙”满足集合律4。

定义2 设“⊙”是非空集合A上的二元运算，如果对任意的a,b∈A，有a⊙b=b⊙a，则称运算“⊙”满足交换律5。

定义3 设(A；*，⊙)是一代数系统，如果对任意的a、b、c∈A，有

(1)a*(b⊙c)=(a*b)⊙(a*c)，则称“*”对“⊙”有左分配律；

(2)(b⊙c)*a=(b*a)⊙(c*a)，则称“*”对“⊙”有右分配律5。