[科普中国]-拉格朗日乘子法

定义

对于具有l个等式约束的n维优化问题

,

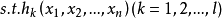
把原目标函数 改造成为如下形式的新的目标函数

式中的 就是原目标函数 的等式约束条件，而待定系数 称为拉格朗日乘子。这种方法称为拉格朗日乘子法。

在极值点处，有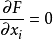 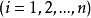和 ，共有n+l个方程，足以算出这n+l个变量，此法也称为升维法。1

基本原理拉格朗日乘子法是一种经典的求解条件极值的解析方法，可将所有约束的优化模型问题转化为无约束极值问题的求解。一般带不等式约束的最优化问题求解如下式：

拉格朗日乘子法是用于变量无关的是常数 分别乘各约束函数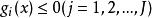 并与目标函数相加得到如下的拉格朗日函数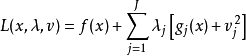： ，式中： 为自变量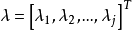； 为拉格朗日乘子量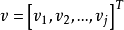； 为松弛变量。

则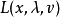 在 处取极值的必要条件为： ，依据上式求得 即为最优解。2

计算过程1.假设需要求极值的目标函数(objective function)为f(x,y)，限制条件为φ(x,y)=M

2.设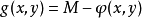

3.定义一个新函数

4.用偏导数方法列出方程：

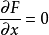
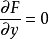
5.求出x,y,λ的值，代入即可得到目标函数的极值1

参数λ的含义（1） 是由参数M所引起的约束条件变化时，对目标函数最优值影响的度量；或者说表示了最优值的“灵敏度”。

（2）当约束条件M增加一个单位时，目标函数值f将近单位。

（3）在经济学上参数 表示产品或资源M增加一个单位时，所带来的最大社会效益f，常称为“边际效益”或“临界值”，在商业经营决策中很有用处。3

直观意义引理1如果函数 是光滑的，并且 是 的一个正则点（即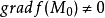 ），那么， 垂直于过 的 的等值线。4

引理2在等值面 上的每个正则点 ，向量 垂直于等值面，并且这个向量是唯一4的（不计其某一常数倍）。

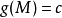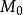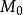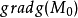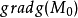定理假设 在曲面S: 上的点 有最大（小）值，并且 不是 的临界点（g的三个偏导数都等于零的点叫g的临界点），则 平行于 ，即存在某个常数 ，使 =。4

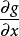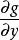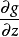部分应用在条件最值中的应用设的最值存在，且，，在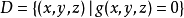上时不同时为零，则最值点必是极值点，从而必是Lagrange函数的驻点。

在不等式证明中的应用设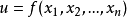在条件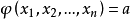之下的最大值为B(a)，则。

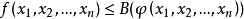在求隐函数极值中的应用5

实际用途假设目标函数代表一个工厂生产产品的数量，约束条件限制了生产中投入的原料和人力的总成本，我们求目标函数的极值，就是要求在成本一定的条件下，如何分配利用人力和原料，从而使得生产量达到最大。此时λ便代表，当成本条件改变时，工厂可达到的生产量最大值的变化率。