[科普中国]-次数

单项式的次数概念

一个单项式中，所有字母的指数的和叫做这个单项式的次数。1

表示法例如，在单项式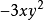中，字母x与y的指数和是x的次数1加上y的次数2等于3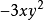，是三次单项式。

在单项式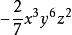中，字母x，y与z的指数和是x的次数3加上y的次数6再加上z的次数2等于11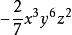．。的次数是11。

性质单项式的次数只与字母的指数有关，例如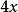，中x的指数为1，这个单项式的次数就是1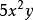；的次数为1+2=3，单独一个数看成单项式时，它的次数为0。

用例求单项式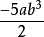的系数、次数是多少？

解: 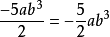，它的系数是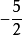，单项式的次数是1+3=4。

相关概念单项式

如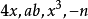，它们都是数与字母的积，这样的代数式叫做单项式。单独一个数或一个字母也是单项式。例如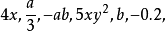，…都是单项式，在单项式中，数与字母，字母与字母间的运算只能是乘法运算，因此分母不能含有字母，由于除以一个数等于乘以这个数的倒数，那么如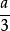看成与a的积，它是单项式。

单项式的系数

由于单项式是由数与字母的积组成的，其中的数称为常数因式，叫做这个单项式的系数。如果一个单项式只含有字母因数，它的系数就是1或者-1．如单项式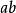，系数是1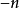；的系数是-1。单项式的系数应包括它前面的符号，例如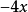，的系数是-4。

系数为1时，通常不写，例如，b的系数为1，系数为-1时，通常只写负号，例如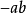，的系数是-1，单独一个数看成单项式时，系数是它本身。

单项式中的数字因数，如，单项式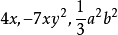的系数分别是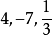。1

多项式的次数概念多项式的每一项都有次数，其中次数最高的项的次数，就是这个多项式的次数。1

表示法例如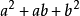：是二次三项式。

用例求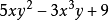的次数。

解: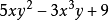中三项次数分别为3、4、0，这个多项式的次数就是4。

相关概念多项式

几个单项式的和叫做多项式，用多项式表示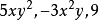的和，则其多项式是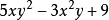。1

多项式的项

在多项式中，每个单项式叫做这个多项式的项，其中不含字母的项叫做常数项，一个多项式含有几项就叫几项式，一个多项式含有几项，就叫几项式，如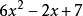是三项式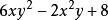，的常数项是8。1