[科普中国]-最概然速率

定义

速率分布曲线有一个高峰（如图1），即速率分布函数 有一个极大值。与 极大值对应的速率叫做最概然速率，通常用 表示。它的物理意义是，如果把整个速率范围(从0到∞)划分成许多相等的小区间，则分布在 所在区间内的分子数的比率最大。 的大小由气体的温度T和摩尔质量 决定。由麦氏速率分布律可以求出 与T和 的关系为

这说明，温度越高， 越大，速率分布曲线的高峰向速率大的一方移动；气体的摩尔质量越大， 越小，速率分布曲线的高峰向速率小的一方移动。2

相关概念在气体内部，所有的分子都以不同的速率运动着，有的分子速率大，有的分子速率小，而且由于相互碰撞，每个分子的速率都在不断地改变。所以，如果在某一特定的时刻去观察某一特定的分子，那么它具有多大的速率完全是偶然的。然而，在一定的条件下，大量分子的速率分布却遵从着一定的统计规律。表1中列出的是用实验方法测量在某一温度下银蒸气分子(银原子)速率分布所得到的数据。实验时把镀银层划分成许多连续的狭条形区域并测出每一区域中银的相对沉积量，因而结果就得到在不同速率区间(如 )内分子数 所占总分子数 的百分比 。

|| || 表1

显然，我们可以把上表所列的数据画成图1(像在计划统计部门常见到的一些挂图)，把银分子的速率分布情况更形象、直观地表示出来。在图1中横坐标是速率v(以 为单位)，每个狭长矩形的底边对应于一个速率区间 ，每个矩形的面积表示分布在该区间内的分子数 占总分子数 的百分比 ，因而纵坐标则表示分布在单位速率区间内的分子数占总分子数的百分比 。

不难想象，如果在实验时把镀银狭条分割得更细，即把速率区间 划分得更小，则在图1中所得到的一些狭长矩形将变得更窄。在极限情形下，图1中各矩形上顶边的连线将变成如图2所示的光滑曲线。显然，这样的图线能更精确地反映气体分子的速率分布情况。

实际上，在测定气体分子速率的实验获得成功之前英国物理学家麦克斯韦(1831一1879)等人已从理论上确定了平衡态下气体分子按速率分布的统计规律。这个规律叫做麦克斯韦速****率分布律，或简称麦氏速率分布律。由麦氏速率分布律所确定的气体分子的速率分布情况与实验结果能很好地吻合，麦氏速率分布律的解析表达式比较复杂，在这里不作介绍。由解析表达式可以画出精确反映气体分子速率分布的图线，如图2。这种图线叫做麦氏速率分布曲线。2

速率分布函数在图2中，与不同速率 对应的纵坐标 有不同的值。也就是说，纵坐标 是 的函数，因此可以令

叫做速率分布函数。

在 和定义式 中， 是总分子数， 是分布在某一速率间隔 曲内的分子数， 是分布在这一速率间隔内的分子数占总分子数的比率， 是速率间隔的大小，所以 表示分布在速率v附近单位速率间隔内分子数占总分子数的比率。这就是速率分布函数的物理意义。速率分布函数是一个普遍的概念。气体分子在不同的条件下有不同的速率分布函数，麦氏速率分布律则在于给出了气体分子在平衡态下的速率分布函数。

麦氏速率分布曲线的特征由图1可见，速率分布曲线从坐标原点出发，经过一极大值后，随速率的增大而趋近于横坐标轴。这说明气体分子的速率可以取0到∞之间的一切数值；速率很大和很小的分子所占的比率都很小，而具有中等速率的分子所占的比率却很大。由速率分布函数的定义式 可知，图1中任一速率间隔 内曲线下的狭条面积等于

它表示分布在这个速率间隔内的分子数占总分子数的比率。而任一有限区间 内曲线下的面积等于

表示分布在这个速率区间内分子数的比率。

现在进一步考虑速率分布曲线下的总面积等于多少。由以上讨论可知，曲线下的总面积为

它表示速率分布在0到 整个速率范围r内的分子数占总分子数的比率，它显然应等于1。即

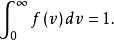这个结论是由速率分布函数的物理意义所决定的，它是速率分布函数所必须满足的条件。2