[科普中国]-图着色问题

简介

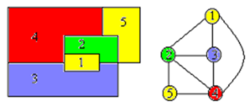
图的m-着色判定问题——给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色，是否有一种着色法使G中任意相邻的2个顶点着不同颜色?

图的m-着色优化问题——若一个图最少需要m种颜色才能使图中任意相邻的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的最小色数m的问题称为m-着色优化问题。1

路线着色问题G是一个有限有向图并且G的每个顶点的出度都是k。G的一个同步着色满足以下两个条件：

1)G的每个顶点有且只有一条出边被染成了1到k之间的某种颜色；

2)G的每个顶点都对应一种走法，不管你从哪里出发，按该走法走，最后都结束在该顶点。

有向图G存在同步着色的必要条件是G是强连通而且是非周期的。一个有向图是非周期的是指该图中包含的所有环的长度没有大于1的公约数。路线着色定理这两个条件(强连通和是非周期)也是充分的。也就是说,有向图G存在同步着色当且仅当G是强连通而且是非周期的。

道路着色问题（Road Coloring Problem）是图论中最著名的猜想之一。通俗的说，这个猜想认为，可以绘制一张“万能地图”，指导人们到达某一目的地，不管他们原来在什么位置。这个猜想最近被以色列数学家艾夫拉汉· 特雷特曼(Avraham Trahtman)在2007年9月证明。

特雷特曼在数学上的这一成果极为令人瞩目，英国《独立报》为此事专门发表了一篇题为“身无分文的移民成了数学超级明星”的文章，给予了高度的评价。

以色列人也为特雷特曼取得的成就感到无比的骄傲。特拉维夫电视台中断了正常的节目播放，以第一时间发布了这一重大消息，连中东其他国家的主流媒体也作了大篇幅的相关报道。

得知特雷特曼解决这一难题的消息后，多年从事路线着色问题研究的加拿大数学家乔尔·弗里德曼说，“路线着色问题的解决令数学共同体非常兴奋。”读过特雷特曼论文的中国数学家和语言学家周海中教授认为，特雷特曼的数学知识非常渊博，解题方法十分巧妙，这一谜题得到破解，无疑是数学史上的一个华彩乐章。

算法点着色问题有简单的时间复杂度为O(3^n)的算法，即设f(S)表示集合的色数，则。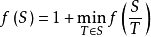

算法描述color[n]存储n个顶点的着色方案，可以选择的颜色为1到m。

当t=1时，对当前第t个顶点开始着色：若t>n，则已求得一个解，输出着色方案即可。否则，依次对顶点t着色1-m， 若t与所有其它相邻顶点无颜色冲突，则继续为下一顶点着色；否则，回溯，测试下一颜色。

#include int color[100];bool ok(int k,int c[][100])//判断顶点k的着色是否发生冲突{ int i,j; for(i=1;i