[科普中国]-平凡解- · 科普中国网

概念

数学中，术语“平凡”（“平凡的”）经常用于结构非常简单的对象（比如群或拓扑空间），有时亦会用明显或乏趣这两个词代替，但对非数学工作者来说，它们有时可能比其他更复杂的对象更难想象或理解。

例如：

明显因数：对于每个正整数 n 来说，1、-1、n 和 -n 都是它的明显因数。

空集：不包含任何元素的集合；

平凡群：只含单位元的群；

平凡环：定义于单元素集合的环。

定义一般，Ax=0中的零解,即x=0，称为平凡解。

矩阵代数的中的定义，AX=0, 行列式|A|≠0, 则X只有平凡解X=0，无非平凡解.

因为任何线性空间的子空间都过零点，所以明显的等于0的时候解是成立的，但这显然没什么意义，说这个0解是平凡的。

通俗来讲，如果方程组AX=0, 只有当X=0的时候才成立，就说方程组AX=0只有平凡解（trivial solution），此时肯定有行列式|A| 不为零。相反如果方程组AX=0存在非零解，也就是说存在不为零的X也可以使方程组AX=0成立，则说方程组AX=0存在非平凡解（nontrivial solution），此时肯定有系数矩阵行列式的值|A|=01。

例如，考虑微分方程：。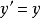

这里y=f(x) 为函数，其导数为y′。

y= 0，0 函数是平凡解；

y(x) = e，指数函数是一个非平凡解。

类似地，数学家经常将费马大定理描述为方程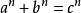对n> 2 没有非平凡解。显然，这个方程确实有解。比如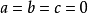对任何n都是解，a= 1,b= 0,c= 1 也一样。但是这种解是显然而无趣的，从而称为平凡解。

扩展数学推理

平凡也经常指证明中容易的情形，为了完整性而不能省略。比如，数学归纳法证明分为两部分：“奠基步骤”是对一个特殊起始值比如n= 0 或n= 1 证明定理；然后归纳步骤证明如果定理对特定值n成立，那么对n+1 也成立。奠基情形经常是显然的。（但是，也有归纳步骤是平凡的而奠基情形却困难的例子。关于多项式的定理经常是这种类型，证明对变元的个数用归纳法。证明如果系数环A是唯一分解整环那么A[X1,...,Xn] 是唯一分解整环，归纳步骤只要简单的写成A[X1,...,Xn] =A[X1,...,Xn-1][Xn]，而一个变元的奠基情形是困难的。）类似地，我们可能想证明某种性质对一个集合中所有元素都成立。证明的主要考虑非空集合，详细检验其元素是否具有该性质；但如果集合是空集，则性质对其所有元素都成立，因为没有元素需要检验。

数学界一个常见的笑话是说“平凡”和“被证明了的”是同义词——这就是说，任何定理如果已知成立就可以认为是“平凡”的。另一个笑话是关于两个数学家讨论一个定理。第一个数学家说某个定理是“平凡的”。另一个要求一个解释，然后他进行了 20 分钟的解说。解说完了之后，第二个数学家同意这个定理是平凡的。这个笑话指出对平凡性判断的主观性。举个例子，对微积分熟练的人，会认为这个定理

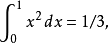是平凡的。但对初学者来说，可能一点也不显然。

值得注意的是，平凡性也取决于语境。泛函分析中的证明可能会给出一个数，平凡地假设存在这样的大数。在初等数论中证明自然数的基本结论时，证明也许会与“每个自然数都有一个后继”息息相关，但此点需加以证明，或者将其作为一个公理。