[科普中国]-欧拉常数

简介

欧拉常数最先由瑞士数学家莱昂哈德·欧拉(Leonhard Euler)在1735年发表的文章 De Progressionibus harmonicus observationes 中定义。欧拉曾经使用C作为它的符号，并计算出了它的前6位小数。1761年他又将该值计算到了16位小数。1790年，意大利数学家马歇罗尼（Lorenzo Mascheroni)引入了γ作为这个常数的符号，并将该常数计算到小数点后32位。但后来的计算显示他在第20位的时候出现了错误。欧拉数以世界著名数学家欧拉名字命名；还有一个鲜为人知的名字纳皮尔常数，用来纪念苏格兰数学家约翰·纳皮尔 (John Napier) 引进对数2。

概述欧拉常数（Euler-Mascheroni constant)

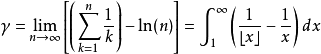
欧拉-马歇罗尼常数(Euler-Mascheroni constant)是一个主要应用于数论的数学常数。它的定义是调和级数与自然对数的差值的极限2。

由无穷级数理论可知，调和级数 是发散的。但可以证明，

存在极限。由不等式 可得

故 有下界。而

再一次根据不等式 ，取 ，即可得

所以 单调递减。由单调有界数列极限定理，可知 必有极限，即

存在。该极限被称作欧拉常数，现在通常将该常数记为γ。

性质与伽玛函数的关系

与黎曼函数的关系

积分

级数展开式

连分数展开式 （OEIS中的数列A002852）。

渐近展开式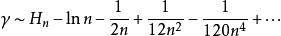

已知位数欧拉常数约为 0.57721566490153286060651209。

目前尚不知道欧拉常数是否为有理数，但是分析表明如果它是一个有理数，那么它的分母位数将超过10242080。1

|| ||

计算方法Xavier Gourdon在1999年使用以下算法计算欧拉常数到了108,000,000位：

对给定的 ，计算：

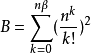
则有

其中，

= 4.970625759544232... 满足方程 。

对给定的，此方法可以得到接近 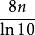位的十进制小数精度。