[科普中国]-光子晶体

光子晶体是指具有光子带隙（PhotonicBand-Gap，简称为PBG）特性的人造周期性电介质结构，有时也称为PBG光子晶体结构。所谓的光子带隙是指某一频率范围的波不能在此周期性结构中传播，即这种结构本身存在“禁带”。

这一概念最初是在光学领域提出的，其研究范围已扩展到微波与声波波段。由于这种结构的周期尺寸与“禁带”的中心频率对应的波长可比拟，所以这种结构在微波波段比在光波波段更容易实现。

基本介绍简介光子晶体（Photonic Crystal）是在1987年由S.John和E.Yablonovitch分别独立提出，是由不同折射率的介质周期性排列而成的人工微结构。光子晶体即光子禁带材料，从材料结构上看，光子晶体是一类在光学尺度上具有周期性介电结构的人工设计和制造的晶体。与半导体晶格对电子波函数的调制相类似，光子带隙材料能够调制具有相应波长的电磁波---当电磁波在光子带隙材料中传播时，由于存在布拉格散射而受到调制，电磁波能量形成能带结构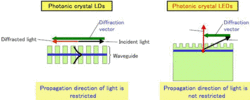。能带与能带之间出现带隙，即光子带隙。所具能量处在光子带隙内的光子，不能进入该晶体。光子晶体和半导体在基本模型和研究思路上有许多相似之处，原则上人们可以通过设计和制造光子晶体及其器件，达到控制光子运动的目的。光子晶体（又称光子禁带材料）的出现，使人们操纵和控制光子的梦想成为可能。

简单地说，光子晶体具有波长选择的功能，可以有选择地使某个波段的光通过而阻止其它波长的光通过其中。

此外值得注意的是，蝴蝶翅膀的颜色在很大程度上与光子晶体有关1，然而这并不意味着蝴蝶翅膀是无色的2。

背景微波波段的逞隙常称为电磁带隙（ElectromagneticBand-Gap,简称为EBG），光子晶体的引入为微波领域提供了新的研究方向。光子晶体完全依靠自身结构就可实现带阻滤波，且结构比较简单，在微波电路、微波天线等方面均具有广阔的应用前景。国外在这一方面的研究已经取得了很多成果，而国内的研究才刚刚起步，所以从事光子晶体的研究具有重要的意义。光子晶体是指具有光子带隙（Photonic Band-Gap，简称为PBG）特性的人造周期性电介质结构，有时也称为PBG结构，其的研究范围已扩展到微波与声波波段。由于这种结构的周期尺寸与“禁带”的中心频率对应的波长可比拟，所以这种结构在微波波段比在光波波段更容易实现。

分类按照光子晶体的光子禁带在空间中所存在的维数，可以将其分为一维光子晶体、二维光子晶体和三维光子晶体，如图。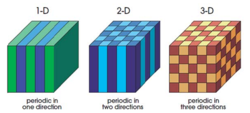

基本原理众所周知，很多的研究都是起源于对自然界不同领域存在类似现象的假设开始的。因为宇宙万物遵循着相同的规律，即使外表再怎样的千变万化，而内在的规则却是有着高度一致性。这正是宇宙的神奇之处，也是人类难解的秘密。光子晶体的产生亦是如此，它是科学家们在假设光子也可以具有类似于电子在普通晶体中传播的规律的基础上发展出来的。

从晶体结构图中，我们可以看出晶体内部的原子是周期性有序排列的，正是这种周期势场的存在，使得运动的电子受到周期势场的布拉格散射，从而形成能带结构，带与带之间可能存在带隙。电子波的能量如果落在带隙中，就无法继续传播。其实，不论是电磁波，还是其它波如光波等，只要受到周期性调制，都有能带结构，也都有可能出现带隙。而能量落在带隙中的波同样不能传播。

简言之，半导体中离子的周期性排列产生了能带结构，而能带又控制着载流子（半导体中的电子或者空穴）在半导体中的运动。相似的，在光子晶体中是由光的折射率指数的周期性变化产生了光带隙结构，从而由光带隙结构控制着光在光子晶体中的运动。

结构光子晶体的结构可以这样理解，正如半导体材料在晶格结点（各个原子所在位点）周期性的出现离子一样，光子晶体是在高折射率材料的某些位置周期性的出现低折射率（如人工造成的空气空穴）的材料。如下图所示的光子晶体材料从一维到三维的结构，可以明显看出周期性的存在，而且三维光子晶体的结构图与普通的硅晶体单从结构是很相似的。高低折射率的材料交替排列形成周期性结构就可以产生光子晶体带隙（BandGap，类似于半导体中的禁带）。而周期排列的低折射率位点的之间的距离大小相同，导致了一定距离大小的光子晶体只对一定频率的光波产生能带效应。也就是只有某种频率的光才会在某种周期距离一定的光子晶体中被完全禁止传播。

如果只在一个方向上存在周期性结构，那么光子带隙只能出现于这个方向。如果在三个方向上都存在周期结构，那么可以出现全方位的光子带隙，特定频率的光进入光子晶体后将在各个方向都禁止传播。这对光子晶体来说是一个最重要的特性。而且实际上，这种三维光子晶体也是最先被制造出来的。

因为光被禁止出现于光子晶体带隙中，所以我们可以预见到我们能够自由控制光的行为。例如，如果我们考虑引入一种光辐射层，该层产生的光和光子晶体中的光子带隙频率相同，那么由于光的频率和带隙一致则禁止光出现于该带隙中这个原则就可以避免光辐射的产生。这就使我们可以控制以前不可避免的自发辐射。

而如果我们通过引入缺陷破坏光子晶体的周期结构特性，那么在光子带隙中将形成相应的缺陷能级。将仅仅有特定频率的光可在这个缺陷能级中出现。这就可以用来制造单模发光二极管和零域值激光发射器（详见光子晶体应用）。而如果产生了缺陷条纹--即沿着一定的路线引入缺陷，那么就可以形成一条光的通路，类似于电流在导线中传播一样，只有沿着“光子导线”（即缺陷条纹）传播的光子得以顺利传播，其它任何试图脱离导线的光子都将被完全禁止。理想状态下我们已经实现了一条无任何损耗的光通路。这种光通路甚至比光纤更有效。

未来研究方向近年来，光子晶体得到了越来越多的关注和推崇。科学家们从各个方面来寻求开发应用光子晶体的途径。然而，光子晶体得到广泛应用，还需要解决以下几个问题：

（1）制作可以对波长在可见光范围内的光产生BandGap的光子晶体还有很大的困难特别是三维光子晶体（具体内容请参看光子晶体制造方法介绍）；

（2）解决随意在任意位置引入需要的缺陷的问题--上文已经提到这种缺陷意义；

（3）制作高效率光子传导材料的技术问题；

（4）如何将已有的电流和电压加到光子晶体上的问题。晶体结构可在外加电场和磁场控制下进行转换从而成为可调节的光子晶体。该种可调节晶体结构的光子晶体可用来制作体积微小、广泛用於遥距通讯和卫星通讯的远红外激光器，亦有助研究激发态分子的化学反应，对化工生产、药物研制及生物科技都十分重要。

固体物理与光子晶体的联系与区别：

固体物理中的许多其它概念也可以用在光子晶体中，不过需要指出的是光子晶体与常规的晶体虽然有相同的地方，也有本质的不同，如光子服从的是麦克斯韦（Maxwell）方程，电子服从的是薛定谔方程；光子波是矢量波，而电子波是标量波；电子是自旋为1/2的费米子，光子是自旋为1的玻色子；电子之间有很强的相互作用，而光子之间没有。

研究与应用应用迄今为止，已有多种基于光子晶体的全新光子学器件被相继提出，包括无阈值的激光器，无损耗的反射镜和弯曲光路，高品质因子的光学微腔，低驱动能量的非线性开关和放大器，波长分辨率极高而体积极小的超棱镜，具有色散补偿作用的光子晶体光纤，以及提高效率的发光二极管等。光子晶体的出现使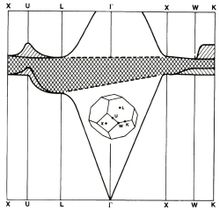信息处理技术的“全光子化”和光子技术的微型化与集成化成为可能，它可能在未来导致信息技术的一次革命，其影响可能与当年半导体技术相提并论。

光子晶体近期在国际上的应用进一步深化，具体表现为：

（1）与纳米技术相结合，用于制造微米级的激光，硅基激光；

（2）与量子点结合，使得原子和光子的相互作用影响材料的性质，从而达到减小光速、减小吸收等作用；

（3）光子晶体光纤应用：随着社会的发展，显赫一时的半导体器件已经不能满足信息技术发展的需要，必须寻找信息传输速率更高，效率更高的新材料。普遍认为，光子技术将续写电子技术的辉煌，光子晶体将成为未来所依赖的新材料；

（5）狄拉克锥在光子晶体中的实现。

制备光子晶体的制备有一定的难度，因为光子晶体的晶格尺度和光的波长具有相同的数量级，如：对于光通信波段（波长1.55μm），要求光子晶体的晶格在 0.5μm左右。近些年来，在人们不断探索和试验的过程中，出现了许多可行的人工制备方法，如：介质棒堆积、精密机械钻孔、胶体颗粒自组织生长、胶体溶液自组织生长和半导体工艺等。用这些方法，通过人工地控制光子晶体中介电材料之间介电常数的配比和光子晶体的微周期性结构，可以制备出带有各种带隙的光子晶体。

理论研究光子晶体的理论研究始于上世纪80年代末期。虽然1987年Yablonovitch和John就提出了光子晶体的概念，但直到1989 年，Yablonovitch和Gmitter首次在实验上证实三维光子能带结构的存在，物理界才开始大举投入这方面的理论研究。由于光子晶体有类似电子晶体的结构，人们通常采用分析电子晶体的方法结构电磁理论来分析光子晶体的特性，并取得了和试验一致的结果。主要的方法有：平面波展开法（planewaveexpansionmethod简称：PWM）、传输矩阵法（transfermatrixmethod简称：TMM）、有限差分时域法（finitedifferencetimedomain简称：FDTD）和散射矩阵法（scatteringmatrixmethod简称：SMM）等。

平面波展开法是比较常用的一种方法，它的基本思想是：将电磁场以平面波的形式展开，可以将麦克斯韦方程组化成一个本征方程，求解该方程的本征值便得到传播光子的本征频率。这种方法的不足之处是当光子晶体结构复杂或处理有缺陷的体系时，可能因为计算能力的限制而不能计算或者难以准确计算。而且如果介电常数不是常数而是随频率变化，就没有一个确定的本征方程形式，这种情况下根本无法求解。

传输矩阵法是将磁场在实空间的格点位置展开，将麦克斯韦方程组化成传输矩阵形式，同样变成本征值求解问题。传输矩阵表示一层（面）格点的场强与紧邻的另一层（面）格点场强的关系，它假设在构成的空间中在同一个格点层（面）上有相同的态和相同的频率，这样可以利用麦克斯韦方程组将场从一个位置外推到整个晶体空间。这种方法对介电常数随频率变化我金属系统特别有效，而且由于传输矩阵小，矩阵元少，运算量小，同时在计算传输光谱时也是十分方便的。但是用该方法求解电磁场的分布较为麻烦，效率不是很高，因此对于光子晶体物理特性的理解没有太大的帮助。

有限差分时域法是电磁场数值计算的经典方法之一。在这里将一个单位原跑划分成许多网状小格，列出网上每个结点的有限差分议程，利用布里渊区边界的周斯条件，同样将麦克斯韦方程组化成矩阵形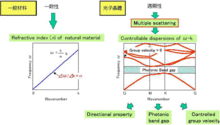式的特征方程，这个矩阵是准对角化的，其中只有少量的一些非零矩阵元，计算最小。但是由于有限差分时域法没有考虑晶格的具体形状，在遇到特殊形状晶格的光子晶体时，很难精确求解。

散射矩阵法假定光子晶体由各向同性的介质组成，其中充满了各种开头和尺寸的没有重叠的光学散射中心。通过对所有的散射中心的散射场应用傅立叶－贝塞尔展开来求解亥姆霍兹方程，从而计算出在光子晶体中传输的场分布。应用这种方法对于求解场分布和传输光谱都是可行的，但是由于这种方法需要较长的运算时间，在有些情形下实际上是不可行的。

实际理论分析中，还有很多其他的方法，如：有限元法、N阶法等。这些方法各有优缺点，在应用时要根据实际场合合理地选用。在光子晶体的研究中这些分析方法是十分重要的，由于光子晶体的制备非常困难，通常是先应用这些方法分析得出光子晶体的一些特性，再由试验来验证这些结论。

未来发展预言总是很难实现。但是，光子晶体电路和装置的未来看起来却是确信无疑的。五年之内，许多光子晶体的基本应用将会在市场上出现。在这些应用中，将会有高效光子晶体激光发射器和高亮度的发光二极管。

而当每个家庭都连接到一个光纤网络的时候，与如今"视顶盒"类似的解码信号设备将使用光子晶体电路和装置而不是笨重的光纤和硅回路。

在五到十年的范围内，我们应该制造出第一个光子晶体"二极管"和"晶体管"；在十到十五年里，我们能制造出第一个光子晶体逻辑电路并使之占有主要地位；在接下来的二十五年内，由光子晶体驱动的光子计算机应该可以制造出来。令人惊奇的是，合成蛋白石甚至可以在珠宝和艺术品市场上找到生存环境；并且光子晶体薄膜能贴在信用卡上作为防伪标志。

如果我们的预言只是完全不可能实现的对未来的歪曲，我们希望大部分人会忘记我们曾经这样说过。然而，光子晶体的未来看起来还是充满光明的。

本词条内容贡献者为:

唐浩宇 - 教授 - 湘潭大学