[科普中国]-傅里叶积分

概念

傅里叶积分是一种积分在运算过程中的变换，它来源于函数的傅里叶积分表示。以傅里叶变换为工具，研究函数的许多性质，是傅里叶分析的主要内容。傅里叶变换在数学、物理以及工程技术中都有重要的应用。1

定义一.基本定义和定理基本定义：若函数 f(x)满足条件

①在任一有限区间都连续或只有有限个第一类间断点，并且只有有限个极值；

②在(-∞，+∞)上绝对可积，即有限；则定义[f(x)→C(ω)]

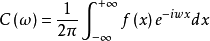
为 f(x)的（复）傅里叶变换；记C(ω) = F[ f (x)] = f (ω)，称 C(ω)为（复）傅里叶变换像函数。

定理：在上面定义的基础上，可以证明

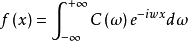
（在间断点，右边的积分收敛到f(x)在该点左右极限的平均值）．称该积分为 f(x)的傅里叶复积分；f(x)为 C(ω)的（傅里叶逆变换 C(ω)→f(x)）原函数。常记。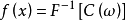

二. 实数形式的傅里叶积分和定理对应的实函数形式为：

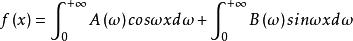称 f(x)的（实数形式的）傅里叶积分。其中

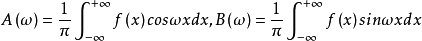称为 f(x)的实傅里叶变换。