[科普中国]-生长曲线函数

生长曲线

技术和经济的发展过程类似于生物的发展过程，经历发生、发展、成熟三个阶段，而每一阶段的发展速度是不一样的。一般的，在发生阶段，变化速度较为缓慢；在发展阶段，变化速度加快；到成熟阶段，变化速度又趋缓慢。按照这三个阶段发展规律得到的事物变化发展曲线，通常称为生长曲线或增长曲线，亦称逻辑增长曲线。由于此类曲线常似“S"型，故又称为S曲线。现在S曲线已广泛用于描述及预测生物个体生长发育及某些技术、经济特性的发展领域中。

生长曲线函数是描述生长曲线的数学表达式。随预测对象的性质不同，生长曲线有很多数学模型，其中应用较广泛的有皮尔（R.Pearl）模型、林德诺（L.Ridenour）模型和龚帕兹（B.Gompertz）模型三种。

生长曲线函数模型生长曲线函数模型，也被称为 Logistic 函数模型，或生长（S）曲线法，简称生长曲线模型，在现代商业、生产行业、生物科学等方面有着非常广泛的应用。生长曲线模型可以表达为：

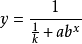
其中，x 为自变量，y 为因变量；k 、a 、b 是未知数（k，a>0，b≠ 1）。

生长曲线模型整体呈现“S”型，可以分为初期、中期和末期三个阶段：

（1）在初期，虽然 x 处于增长阶段，但是 y 的增长较为缓慢，这时曲线呈现较为平缓的上升；

（2）在中期，随着 x 的增长，y 的增长速度逐渐增快，曲线呈现快速上升的态势；

（3）当达到拐点(X*，Y*)后，因函数饱和程度的增长达到末期，随着 x 的增长 y 的增长较为缓慢，增长速度趋近于0，曲线呈水平状发展1。

皮尔模型皮尔曲线是1938年比利时数学家哈尔斯特(P．F verhulst)首先提出的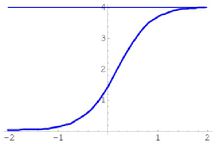一种特殊曲线。后来，近代生物学家皮尔(R．Pearl)和L·J·Reed两人把此曲线应用于研究人口生长规律。所以这种特殊的曲线称之为皮尔增长曲线，简称皮尔曲线。当经济变量的发展变化表现为初期增长速度缓慢，随后增长速度逐渐加快，达到一定程度后又逐渐减慢，最后达到饱和状态的趋势，即原时间序列倒数的一阶差分的环比为一个常数，可以用皮尔曲线来描述。因此，皮尔曲线的预测法是根据预测对象具有皮尔曲线变动趋势的历史数据，拟合成一条皮尔曲线，通过建立皮尔曲线模型进行预测的方法。

皮尔生长曲线的一般模型为：

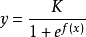
式中，K为常数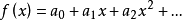， 。常用的皮尔生长曲线模型为（式1）：

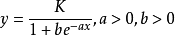
这时，f(x)是x的线型函数，且具有负斜率，如图1所示。

其中，a、b、K为皮尔模型的参数，估算这三个参数的方法有两类：一类是先估算出a和K，然后推算b值，如Fisher法；另一类是同时估算出参数a、b、K，如倒数总和法。

林德诺模型林德诺生长曲线模型常用于新技术发展和新产品销售的预测，其数学模型的一般形式为（式2）：

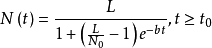
其中，N(t)为t时熟悉新产品的人数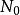； 为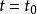 时熟悉新产品的人数；b为校正系数；L为N(t)的极限值。

林德诺模型是基于下述假设条件建立的：新产品的推广或熟悉新产品的人数的增长率与已熟悉新产品的人数和未熟悉新产品的人数的乘积成正比，即满足微分方程：

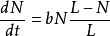
上式在区间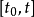 上的积分得式2。由于N(t)与式1中y的表达式实际上相同，故参数的确定方法与皮尔模型类似。

龚帕兹模型龚帕兹 (生长 )曲线是一种常用曲线，其形式为：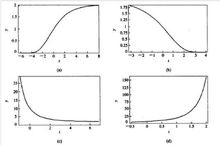

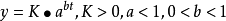
对参数 a、b、K 的不同取值，龚帕兹模型有不同的形状和变化趋势，如图2所示。

（1）图 2-(a) 为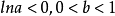 时的龚帕兹曲线；

（2）图 2-(b) 为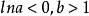 时的龚帕兹曲线；

（3）图 2-(c) 为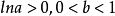 时的龚帕兹曲线；

（4）图 2-(d)为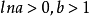 时的龚帕兹曲线。

给定时间序列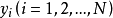，只要求得其中的三个参数值 a、b、K，就可以用来求得未来周期的预测值。

求参数 a、b、K 的方法有多种，如非线性回归分析、特殊函数的最小二乘法等。