[科普中国]-笛卡尔坐标系

简介

笛卡尔坐标系就是直角坐标系和斜角坐标系的统称。 相交于原点的两条数轴，构成了平面放射坐标系。如两条数轴上的度量单位相等，则称此放射坐标系为笛卡尔坐标系。两条数轴互相垂直的笛卡尔坐标系，称为笛卡尔直角坐标系，否则称为笛卡尔斜角坐标系。需要指出的是，请将数学中的笛卡尔坐标系与电影《异次元杀阵》中的笛卡尔坐标相区分，电影中的定义与数学中定义有出入，请勿混淆。

二维的直角坐标系是由两条相互垂直、0 点重合的数轴构成的。在平面内，任何一点的坐标是根据数轴上对应的点的坐标设定的。在平面内，任何一点与坐标的对应关系，类似于数轴上点与坐标的对应关系。采用直角坐标，几何形状可以用代数公式明确的表达出来。几何形状的每一个点的直角坐标必须遵守这代数公式。

平面直角坐标系二维的直角坐标系通常由两个互相垂直的坐标轴设定，通常分别称为 x-轴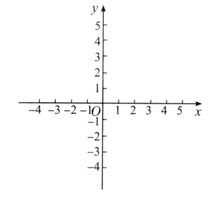和 y-轴；两个坐标轴的相交点，称为原点，通常标记为 O ，既有“零”的意思，又是英语“Origin”的首字母。每一个轴都指向一个特定的方向。这两个不同线的坐标轴，决定了一个平面，称为 xy-平面，又称为笛卡尔平面。通常两个坐标轴只要互相垂直，其指向何方对于分析问题是没有影响的，但习惯性地（见右图），x-轴被水平摆放，称为横轴，通常指向右方；y-轴被竖直摆放而称为纵轴，通常指向上方。两个坐标轴这样的位置关系，称为二维的右手坐标系，或右手系。如果把这个右手系画在一张透明纸片上，则在平面内无论怎样旋转它，所得到的都叫做右手系；但如果把纸片翻转，其背面看到的坐标系则称为“左手系”。这和照镜子时左右对掉的性质有关。

为了要知道坐标轴的任何一点，离原点的距离。假设，我们可以刻画数值于坐标轴。那么，从原点开始，往坐标轴所指的方向，每隔一个单位长度，就刻画数值于坐标轴。这数值是 刻画的次数，也是离原点的正值整数距离；同样地，背着坐标轴所指的方向，我们也可以刻画出 离原点的负值整数距离。称 x-轴刻画的数值为 x-坐标，又称横坐标，称 y-轴刻画的数值为 y-坐标，又称纵坐标。虽然，在这里，这两个坐标都是整数，对应于坐标轴特定的点。按照比例，我们可以推广至实数坐标 和其所对应的坐标轴的每一个点。这两个坐标就是直角坐标系的直角坐标，标记为(x，y)。

任何一个点 P 在平面的位置，可以用直角坐标来独特表达。只要从点 P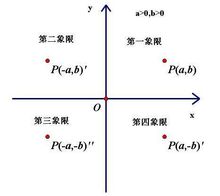画一条垂直于 x-轴的直线。从这条直线与 x-轴的相交点，可以找到点 P 的 x-坐标。同样地，可以找到点 P 的 y-坐标。这样，我们可以得到点 P 的直角坐标。

直角坐标系也可以推广至三维空间（3 dimension）与高维空间 (higher dimension) 。

直角坐标系的两个坐标轴将平面分成了四个部分，称为象限，分别用罗马数字编号为Ⅰ，Ⅱ，Ⅲ，Ⅳ。依照惯例，象限Ⅰ的两个坐标都是正值；象限Ⅱ的 x-坐标是负值， y-坐标是正值；象限Ⅲ的两个坐标都是负值的；象限Ⅳ的 x-坐标是正值， y-坐标是负值。所以，象限的编号是按照逆时针方向，从象限Ⅰ编到象限Ⅳ。

空间笛卡尔坐标系放射坐标系和笛卡尔坐标系平面向空间的推广：相交于原点的三条不共面的数轴构成空间的放射坐标系。三条数轴上度量单位相等的放射坐标系被称为空间笛卡尔坐标系。三条数轴互相垂直的笛卡尔坐标系被称为空间笛卡尔直角坐标系，否则被称为空间笛卡尔斜角坐标系。

空间直角坐标系为了沟通空间图形与数的研究，我们需要建立空间的点与有序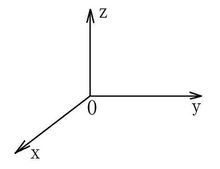数组之间的联系，为此我们通过引进空间直角坐标系来实现。 过定点O，作三条互相垂直的数轴，它们都以O为原点且一般具有相同的长度单位.这三条轴分别叫做x轴(横轴）、y轴(纵轴)、z轴(竖轴)；统称坐标轴.通常把x轴和y轴配置在水平面上，而z轴则是铅垂线；它们的正方向要符合右手规则，即以右手握住z轴，当右手的四指从正向x轴以π/2角度转向正向y轴时，大拇指的指向就是z轴的正向，这样的三条坐标轴就组成了一个空间直角坐标系，点O叫做坐标原点。这样就构成了一个笛卡尔坐标。

在三维笛卡尔坐标系中，三个平面，xy-平面，yz-平面，xz-平面，将三维空间分成了八个部分，称为卦限(octant) 空。第Ⅰ卦限的每一个点的三个坐标都是正值。

笛卡尔和笛卡尔坐标系的产生据说有一天，法国哲学家、数学家笛卡尔生病卧床，病情很重，尽管如此他还反复思考一个问题：几何图形是直观的，而代数方程是比较抽象的，能不能把几何图形与代数方程结合起来，也就是说能不能用几何图形来表示方程呢？要想达到此目的，关键是如何把组成几何图形的点和满足方程的每一组“数”挂上钩，他苦苦思索，拼命琢磨，通过什么样的方法，才能把“点”和“数”联系起来。突然，他看见屋顶角上的一只蜘蛛，拉着丝垂了下来，一会功夫，蜘蛛又顺着丝爬上去，在上边左右拉丝。蜘蛛的“表演”使笛卡尔的思路豁然开朗。他想，可以把蜘蛛看做一个点，它在屋子里可以上、下、左、右运动，能不能把蜘蛛的每个位置用一组数确定下来呢？他又想，屋子里相邻的两面墙与地面交出了三条线，如果把地面上的墙角作为起点，把交出来的三条线作为三根数轴，那么空间中任意一点的位置就可以用这三根数轴上找到有顺序的三个数。反过来，任意给一组三个有顺序的数也可以在空间中找出一点P与之对应，同样道理，用一组数（x、y）可以表示平面上的一个点，平面上的一个点也可以有用一组两个有顺序的数来表示，这就是坐标系的雏形。

直角坐标系的创建，在代数和几何上架起了一座桥梁，它使几何概念用数来表示，几何图形也可以用代数形式来表示。由此笛卡尔在创立直角坐标系的基础上，创造了用代数的方法来研究几何图形的数学分支——解析几何， 他大胆设想：如果把几何图形看成是动点的运动轨迹，就可以把几何图形看成是由具有某种共同特征的点组成的。举一个例子来说，我们可以把圆看作是动点到定点距离相等的点的轨迹，如果我们再把点看作是组成几何图形的基本元素，把数看作是组成方程的解，于是代数和几何就这样合为一家人了。

笛卡尔坐标系的电影定义在电影《异次元杀阵》系列中，笛卡尔坐标的定义有所差别。电影主要讲述的是若干人身处一个神秘密室（cube），密室是一个正方体，上下左右前后都有一道门，可以通往隔邻的另一密室，只有通过特定的方式才能逃离这个地方。Cube由一个巨大的立方体以及包在立方体外的一层外壳组成，两者之间存在一定空间，大立方体内还包含许多小立方体房间，类似于魔方。Cube只有一个出口，只有到达了连接外壳与内部立方体的那个房间才能走出Cube，这个房间在影片中被称为“桥”。每一个房间棱长14尺（略长于4米）。大立方体每条边有26个房间的长度，所以一共是26*26*26=17576个房间的大小。（但事实上没有那么多房间，因为房间要移动必须留有一定的空间）

Cube中的每一个房间都标有三个三位数的数字。这三个三位数即构成了电影中所说的房间的笛卡尔坐标。电影中的笛卡尔坐标，它表示了点在空间中的位置，但却和直角坐标有区别，两种坐标可以相互转换。举个例子：某个点的笛卡尔坐标是493 ,454, 967，那它的X轴坐标就是4+9+3=16，Y轴坐标是4+5+4=13，Z轴坐标是9+6+7=22，因此这个点的直角坐标是(16, 13, 22)。

在电影中，所有的房间并非完全不动的，其运动规律也隐含在其笛卡尔坐标中。比如坐标为477, 804, 539的房间，它的直角坐标为(18, 12, 17)。对于每一个三位数数字作如下处理：

1. 百位数减去十位数
2. 十位数减去个位数
3. 个位数减去百位数
   对三个数字都进行以上操作，也就是：
4. 477:4 - 7=-3 | 7-7=0 | 7-4=3
5. 804:8 - 0=8 | 0-4=-4 | 4-8=-4
6. 539:5 - 3=2 | 3-9=-6 |9-5=4
   这样就得到了三个向量(- 3, 8, 2)， (0, - 4, - 6)和(3, - 4, 4)。这三个向量表示了这个房间的移动轨迹，将转换成直角坐标的表示房间初始位置的坐标（可以看成向量）依次加上这三个向量，即：
   (18, 12, 17) + (- 3, 8, 2) = (15 ,20, 19)
   (15, 20, 19) + (0, - 4, - 6) = (15, 16, 13)
   (15, 16, 13) + (3, - 4, 4) = (18, 12, 17)
   可以看到经过了三次变化以后又回到了原来的初始坐标(18, 12, 17)。每个房间也就是根据这个规律以(18, 12, 17) --> (15, 20, 19) --> (15, 16, 13) --> (18, 12, 17) -->…的轨迹移动的。

最后需要强调的是，数学中的 笛卡尔坐标系与电影《异次元杀阵》中的笛卡尔坐标的定义存在较大的差异，数学中的直角坐标属于笛卡尔坐标的一种，请勿混淆。（因为笛卡尔坐标系就是直角坐标系和斜角坐标系的统称，直角坐标即为直角坐标系中的笛卡尔坐标）

备注笛卡尔在《方法谈》一书附录的《几何学》这篇论文中，阐述了解析几何的基本原理，创造了笛卡尔坐标系。

在笛卡尔以前，几何和代数是两门科学，几何研究图形，代数研究数。笛卡尔不满意这两门科学孤立研究的抽象性，企图使二者联系起来，并使它们具体化。他通过他所设计的坐标系统标示法，以及他对于变数的深入研究，证明几何问题可以归结为代数问题，在求解时可以运用全部代数方法。从此，变数被引进了数学，成为数学发展中的转折点，为微积分的出现创造了条件。笛卡尔坐标系被广泛地应用在工程技术和物理学领域中1。